[Neural Network]Neural Network 3 - Backpropagation

前面介紹了 neural network 使用 Gradient descent 來找 cost function 的最小值，那這篇要來介紹 neural network 如何使用 Backpropagation 這個演算法讓 neural network 訓練過程中更有效率。

這篇是Neural networks的課程筆記。另外，覺得李宏毅老師的課程也講解的很清楚，所以我會搭配老師的課程內容。李宏毅老師和主要課程使用的符號不太ㄧ樣，但我還是使用他們原本各自的符號。

Gradient Descent

Gradient descent 的目的是要找到 neural network 的 parameters 的最佳解。

Network parameters: $$\theta = {{w_1, w_2,…, b_1, b_2,…}}$$

Gradient: $$\nabla L(\theta) = \begin{bmatrix} \partial L(\theta)/\partial w_1 \ \partial L(\theta)/\partial w_2 \ \vdots \ \partial L(\theta)/\partial b_1 \ \partial L(\theta)/\partial b_2 \ \vdots \end{bmatrix}$$

初始 parameters: $$\theta^0$$，計算 $$\nabla L(\theta^0)$$，則 $$\theta^1 = \theta^0 - \eta \nabla L(\theta^0)$$，接著可以再繼續算出 $$\theta_2, \theta_3…$$

在 neural network 裡 Gradient 的最大問題就是，neural network 有太多的參數，所以這裡我們要介紹的 Backpropagation 就是一個比較有效的計算 Gradient 的演算法。也就是說，Backpropagation 基本上就是 Gradient Descent，但是是一個有效率的演算法。

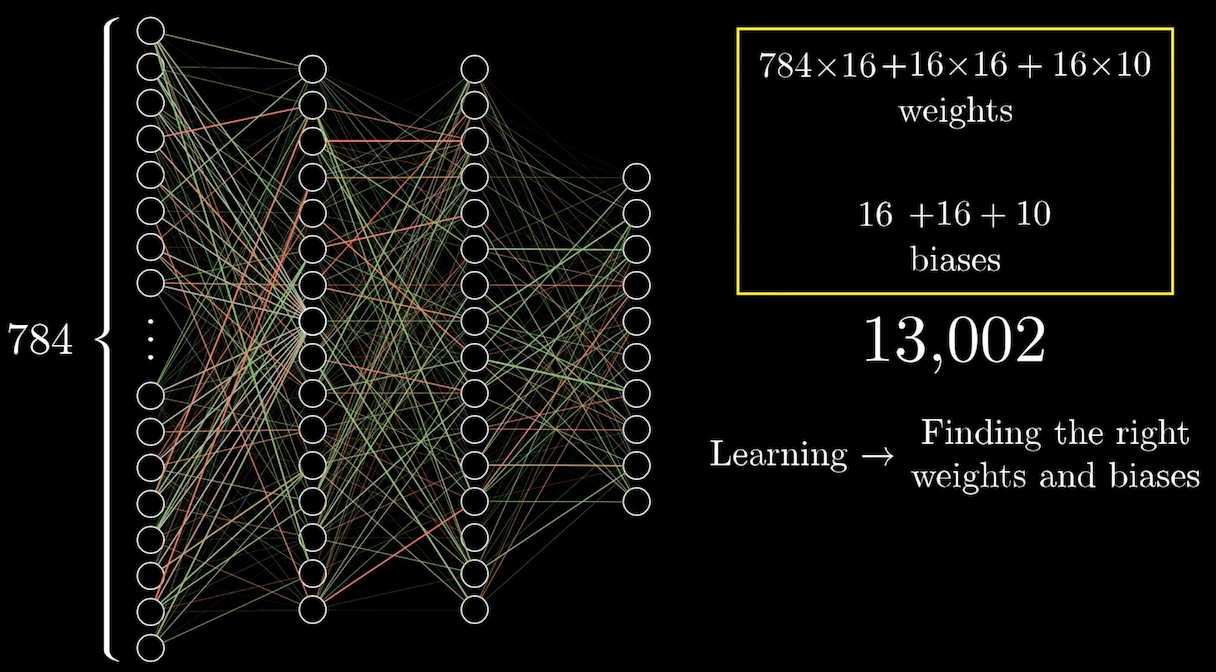
前面我們舉的例子是手寫辨識，input 加上兩層的 hidden layers，總共的 weight 和 bias 加起來有 13,002 個參數。如下圖，


為了講解方便，我們現在把整個 nerual network 簡化成每層只有一個神經元。如下圖，第一個神經元是 input，最後一個神經元是 output，中間是兩層的 hidden layer，所以 cost function 可以寫成，$$C(w_1, b_1, w_2, b_2, w_3, b_3)$$


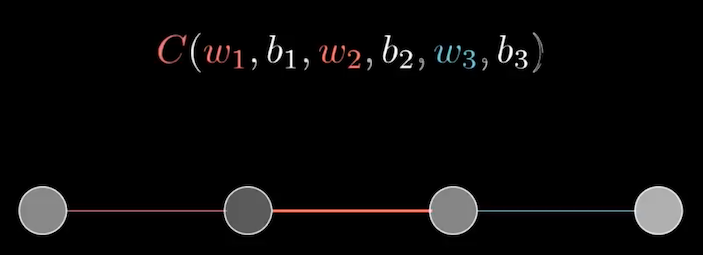
為了說明 Backpropagation 現在我們再把範圍縮小到最後一層的 hidden layer 和 output，如下圖。

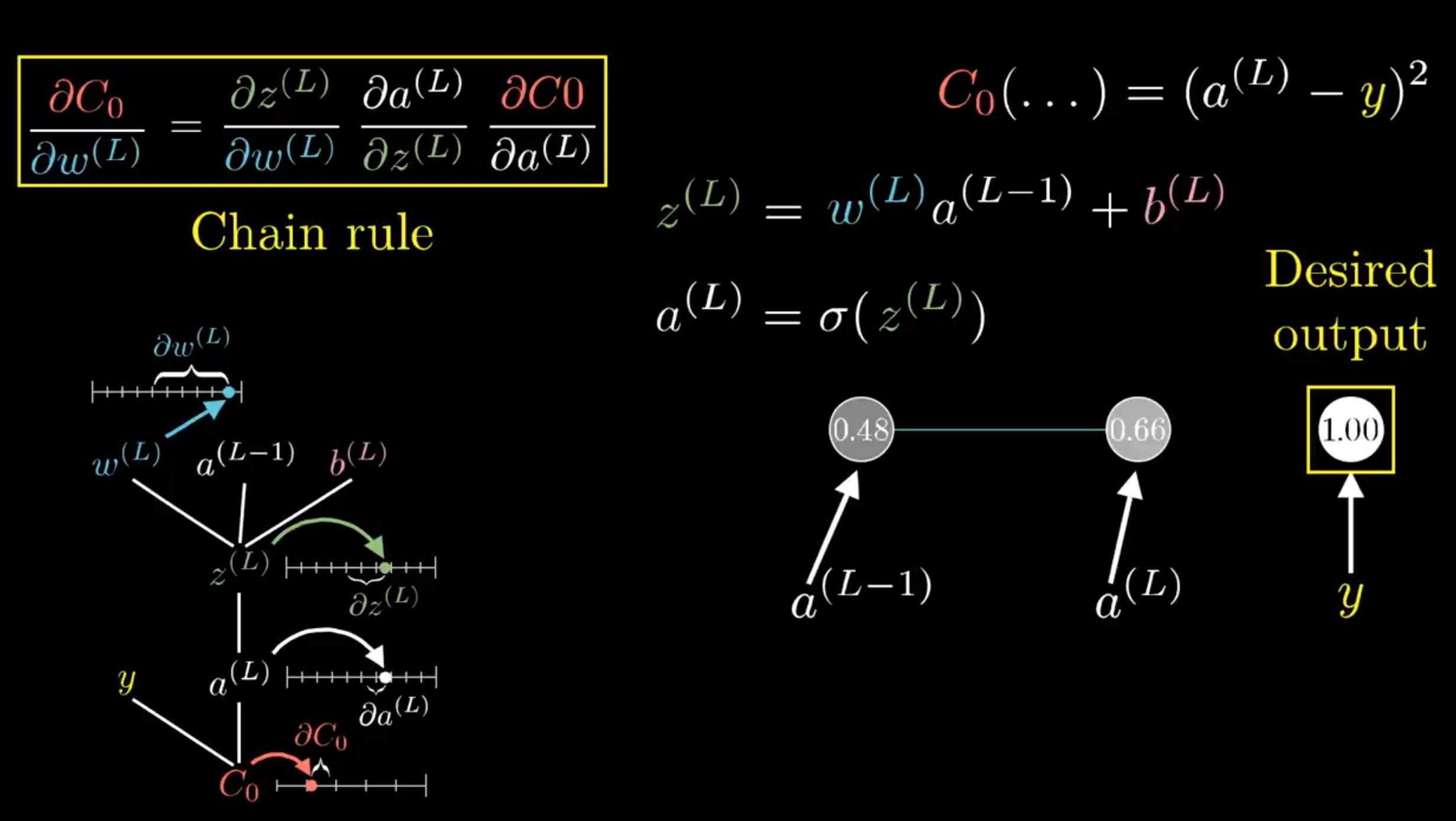
我們令最後的 output 為 $$a^{(L)}$$ 表示它是在第 L 層，而 hidden layer 為 $$a^{(L-1)}$$ 表示在第 L-1 層，所以上標就只是用來表達它們各自在哪一層而已。

在 $$a^{(L-1)}$$ 後的 $$y$$ 是我們期望的輸出結果，我們希望 $$y=1$$，也就是說，這裡的 cost 值會是，

$$C_0(…) = (a^{(L)} - y)^ 2 ………. (1)$$

以上圖的例子就會是，$$(0.66 - 1)^2$$

接著我們來看每一個神經元的值。根據前面學過的，我們知道每一個神經元都是由前面的 weight 和 bias 算出來了，也就是說

$$a^{(L)} = \sigma (w^{(L)} a^{(L-1)} + b^{(L)})$$

那為了方便，我們把 sigmoid function 裡的式子用一個符號表示，

$$z^{(L)} = w^{(L)} a^{(L-1)} + b^{(L)} ………. (2)$$

而 $$a^{(L)}$$ 就可以寫成，

$$a^{(L)} = \sigma (z^{(L)}) ………. (3)$$

我們現在有了上面三個式子，

$$C_0(…) = (a^{(L)} - y)^ 2 ………. (1)$$
$$z^{(L)} = w^{(L)} a^{(L-1)} + b^{(L)} ………. (2)$$
$$a^{(L)} = \sigma (z^{(L)}) ………. (3)$$

那我們現在要如何計算權重 $$w^{(L)}$$ 對於 cost function 的影響程度呢？換句話說，我們想要知道 cost function 對 $$w^{(L)}$$ 的偏微分 $$\frac{\partial C_0}{\partial w^{(L)}}$$。

根據 Chain rule，我們可以再將上式改寫成，

$$\frac{\partial C_0}{\partial w^{(L)}} = \frac{\partial z^{(L)}}{\partial w^{(L)}} \frac{\partial a^{(L)}}{\partial z^{(L)}} \frac{\partial C_0}{\partial a^{(L)}}$$

下一個步驟要來計算每一個值，我們可以根據上面式子得到的 (1)(2)(3) 得到，

$$\frac{\partial C_0}{\partial a^{(L)}} = 2(a^{(L)} - y)$$

$$\frac{\partial a^{(L)}}{\partial z^{(L)}} = \sigma’ (z^{(L)})$$

$$\frac{\partial z^{(L)}}{\partial w^{(L)}} = a^{(L-1)}$$

所以可以將式子整理成，

$$ \begin{align} \frac{\partial C_0}{\partial w^{(L)}} & = \frac{\partial z^{(L)}}{\partial w^{(L)}} \frac{\partial a^{(L)}}{\partial z^{(L)}} \frac{\partial C_0}{\partial a^{(L)}} \ & = a^{(L-1)} \times \sigma’ (z^{(L)}) \times 2(a^{(L)} - y) \end{align} $$

而這只是其中一個 training sample 算出來的 cost，而總代價函數應該是所有 training data 的平均，也就是

$$\frac{\partial C}{\partial w^{(L)}} = \frac{1}{n} \sum_{k=0}^{n-1} \frac{\partial C_k}{\partial w^{(L)}}$$

而這其實只是 gradient 裡其中的一個 compenent，

Gradient:

$$\nabla C = \begin{bmatrix} \frac{\partial C}{\partial w^{(1)}} \ \frac{\partial C}{\partial b^{(1)}} \ \frac{\partial C}{\partial w^{(2)}} \ \frac{\partial C}{\partial b^{(2)}} \ \vdots \ \frac{\partial C}{\partial w^{(L)}} \ \frac{\partial C}{\partial b^{(L)}} \ \end{bmatrix}$$

如果要計算的是 bias 的偏微分，式子就會是，

$$ \begin{align} \frac{\partial C_0}{\partial b^{(L)}} & = \frac{\partial z^{(L)}}{\partial b^{(L)}} \frac{\partial a^{(L)}}{\partial z^{(L)}} \frac{\partial C_0}{\partial a^{(L)}} \ & = 1 \times \sigma’ (z^{(L)}) \times 2(a^{(L)} - y) \end{align} $$

接下來，我們來看這個 cost function 對上一層 activation 的敏感度，

$$ \begin{align} \frac{\partial C_0}{\partial a^{(L-1)}} & = \frac{\partial z^{(L)}}{\partial a^{(L-1)}} \frac{\partial a^{(L)}}{\partial z^{(L)}} \frac{\partial C_0}{\partial a^{(L)}} \ & = w^{(L)} \times \sigma’ (z^{(L)}) \times 2(a^{(L)} - y) \end{align} $$

前面我們看的是只有一個神經元的狀況，回到真實的 neural network 結構。一個神經元是來自前面很多神經元與 weight 和 bias 的計算，且一個 training data 的 cost 值是每個 output 減 expected value 平方的和。



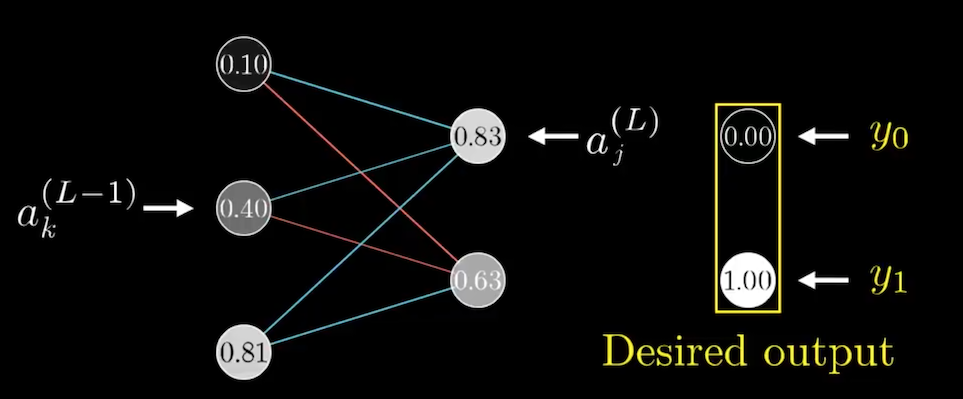
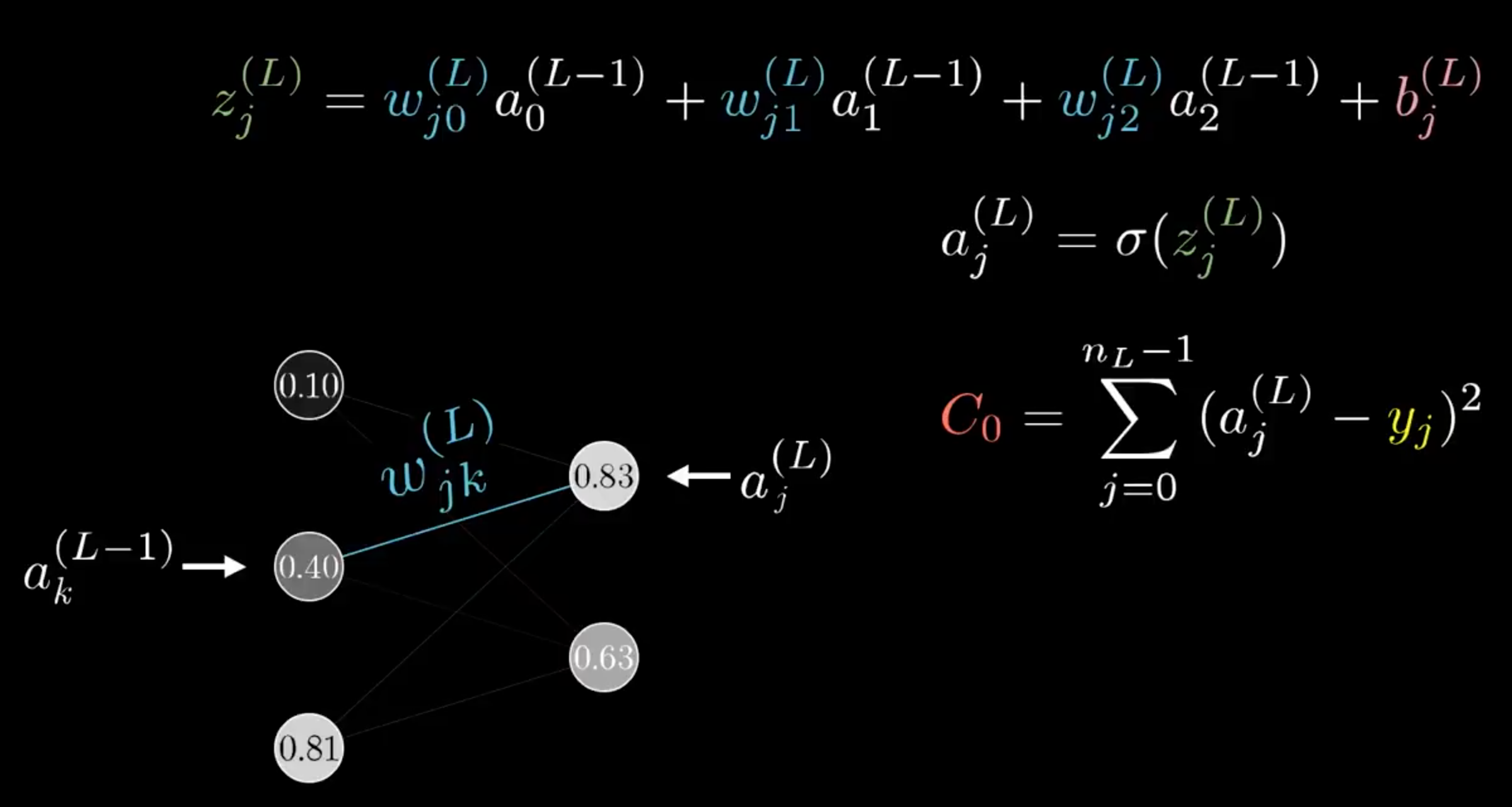
基本上，所有的式子都和只有一個神經元是一樣的，唯一有變化的是，$$\frac{\partial C_0}{\partial a_k^{(L-1)}}$$

$$ \frac{\partial C_0}{\partial a_k^{(L-1)}} = \sum_{j=0}^{n_L-1}\frac{\partial z_j^{(L)}}{\partial a_k^{(L-1)}} \frac{\partial a_j^{(L)}}{\partial z_j^{(L)}} \frac{\partial C_0}{\partial a_j^{(L)}} $$

因為，一個神經元會向下影響其他所有與它連接的神經元，所以必須將它們全部加起來。

根據以上，只要不斷往回算就可以了。

Reference:
ML Lecture 7: Backpropagation
Back-propagation