在了解 CNN (卷積神經網路, Convolutional neural network) 與 RNN (循環神經網絡, Recurrent neural network) 前，先來認識最簡單的 NN (神經網路, Neural network) Multilayer perceptron。

這篇是Neural networks的課程筆記。

---

Neural network 啟發自大腦神經，所謂的 Neural 就是 neurons (神經元)，而在 Neural network 裡，neurons 是個介於 0 和 1 之間的數字。

我們將以讓程式辨認手寫數字 0 到 9 為例解說 Neural network。下圖是一個 28*28 像素的手寫數字，

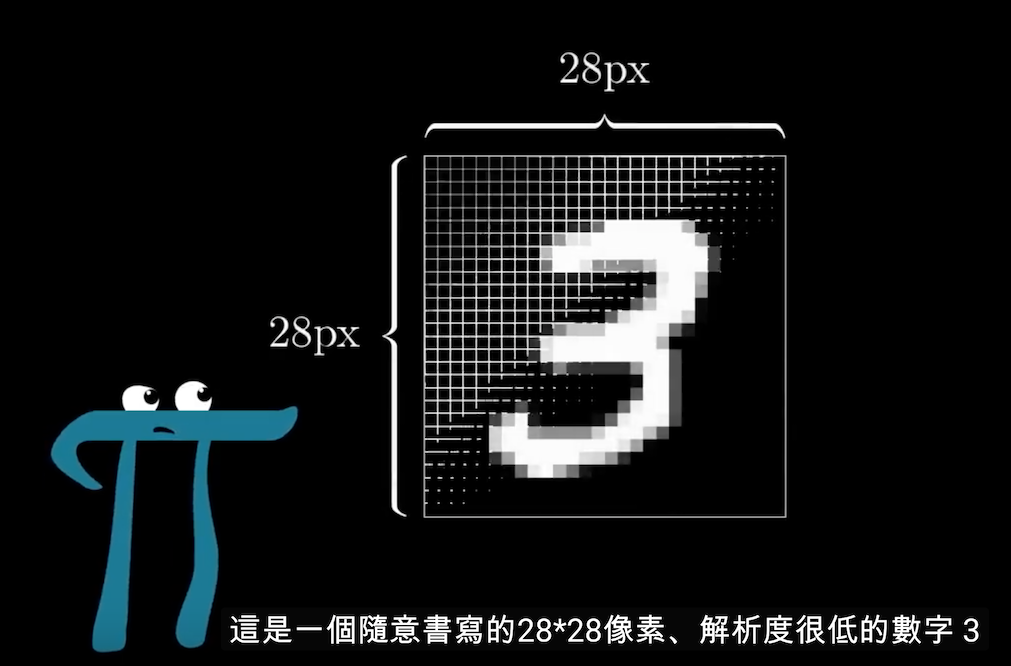
每一個像素都是一個 0 到 1 的灰階值，而 Neural network 以這個圖的每個像素，對應到每個神經元作為輸入值，也就是說第一層輸入層共有 28*28 = 784 個神經元。灰階值 0 為黑色，1 為白色。這些在神經元中的數字稱為「激勵值」（activation）。

這裡範例使用，第一層為輸入層，中間兩層 hidden layers，最後一層為輸出層。而最後輸出層就是 0 到 9 的數字，每個神經元都有個「激勵值」（activation），而這數字就代表著最後給定可能是這個數字的判定結果。

而中間的 hidden layers 正是神經網路的重點。

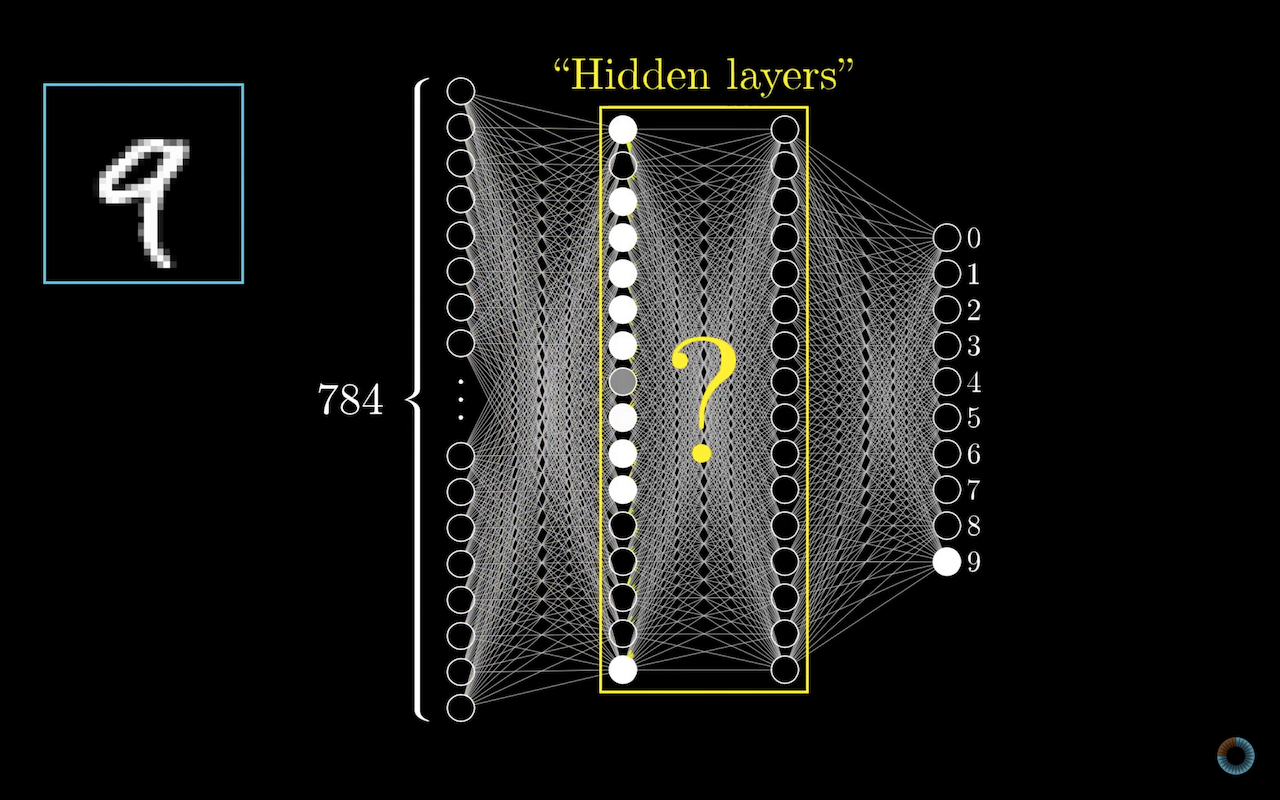
我們可以想像，將整個數字分解成不同的部分，

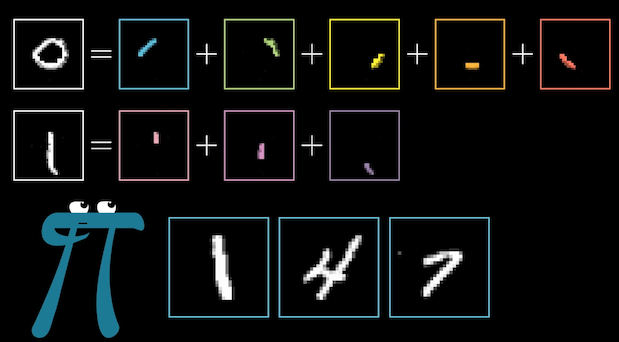
第一層 hidden layer 是比較小段的部分，而第二層 hidden layer 是由這些小區塊組成比較大塊的區塊。

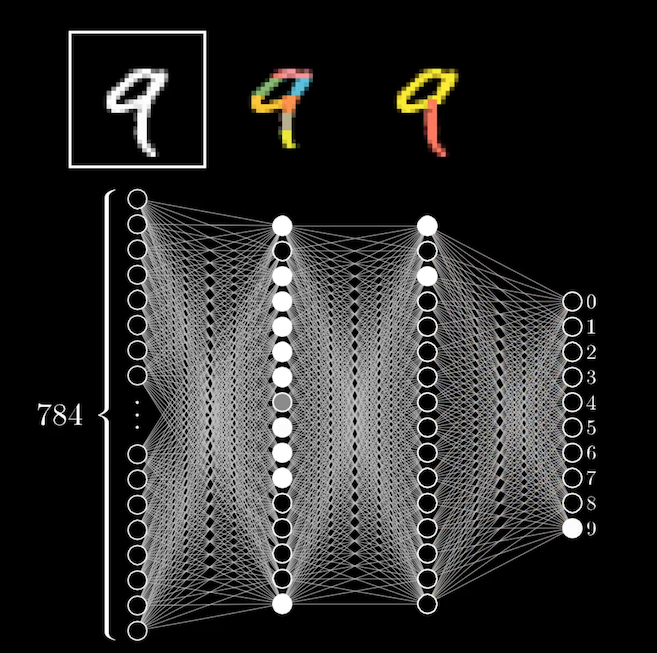
有了這些概念之後，那我們要怎麼從輸入層到第一層的 hidden layer 呢？

現在我們希望，第二層的其中一個神經元可以辨識這個圖有沒有一個邊，如下圖，

我們會給這個神經元與輸入層的神經元之間每個連線一個權重（weight），然後將輸入層的神經元乘上每個權重再加總，權重可以是正或負值。

但因為，我們希望神經元的激勵值（activation）是在 0 和 1 之間，所以使用 sigmoid function \(\sigma(x) = \frac{1}{1+e^x}\) 。經過 sigmoid function 計算，越小的值會越接近 0，越大的值會越接近 1。

但也許並不是每次加總大於零我們就希望給正的灰階值，因此，權重最後再加上個 bias，來調整我們想要給灰階值的值。

所有第一層 hidden layers 的神經元都根據這樣的概念，有自己關注的區塊，有自己的權重，再加上自己的 bias。第二層的 hidden layers 神經元也以同樣的概念計算，所以我們總共會有 13,002 個權重加上 bias。

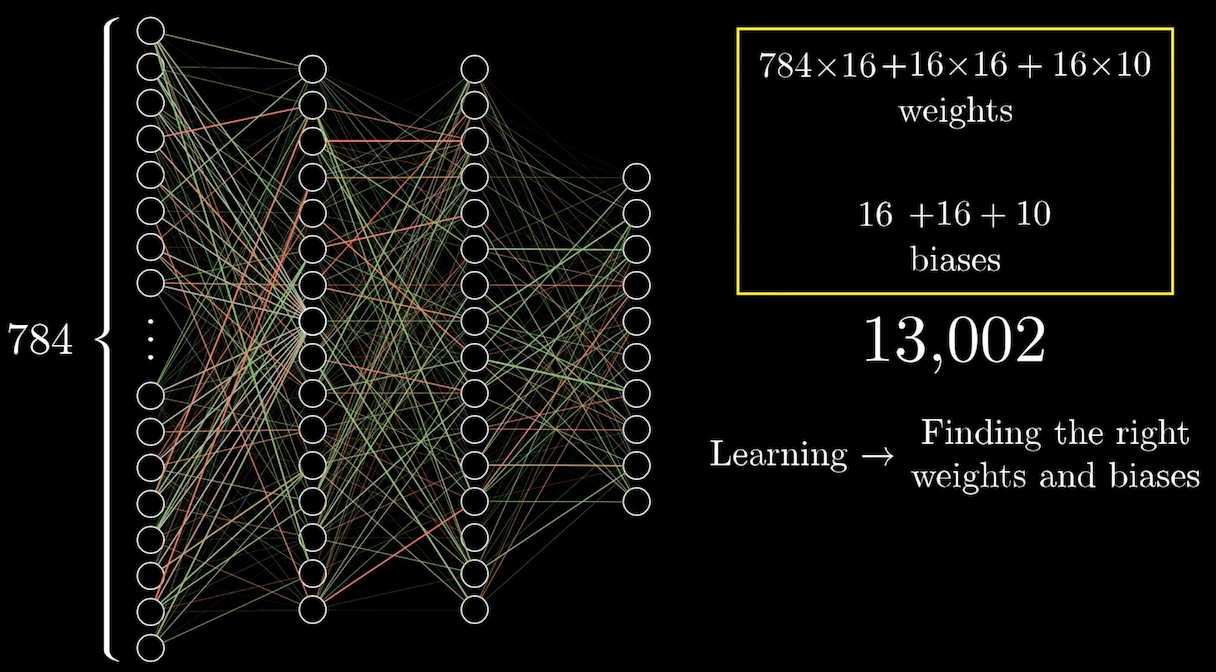
而所謂的 deep learning 的 learning 就是在學習這些權重和 bias，讓電腦去找到正確的值。

上上圖的式子只是其中一個神經元，而我們可以用矩陣表達所有第一層 hidden layers 的神經元。如下圖，

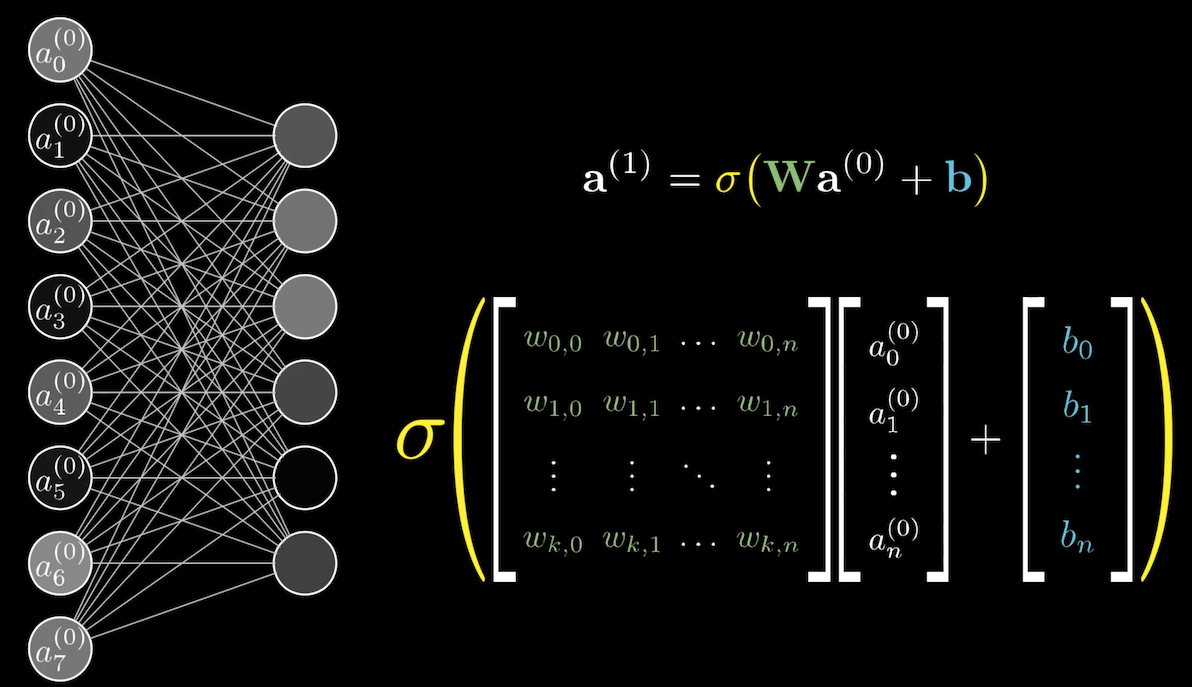
總的來說，我們可以將整個 neural network 看成一個 function。

\[f(a_0, a_1,..., a_{783}) = \begin{bmatrix} y_0 \\ \vdots \\ y_9 \end{bmatrix}\]

最後，其實現在已經不使用 sigmoid function 了，現在主流的 function 用的是 ReLU。

\[ReLU(a) = max(0, a)\]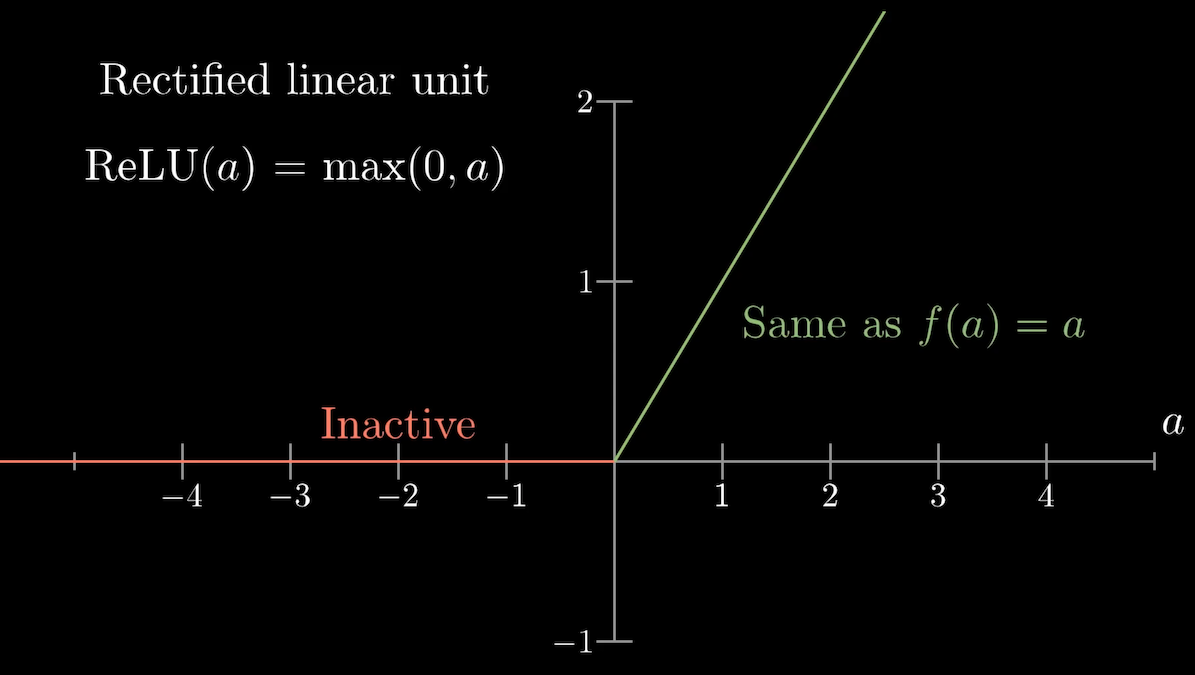

---

Reference:
究竟神經網路是什麼？ 第一章 深度學習