[Neural Network]Neural Network 2 - Gradient descent
上一篇說明了神經網路的基本原理,這篇我們要講解神經網路是如何學習的 - Gradient descent。
這篇是Neural networks的課程筆記。
在 Machine Learning 裡我們使用 training data 訓練得到一個 model,但這「訓練」到底是怎麼訓練的呢?訓練的過程,通常是要找到最小的 cost,也就是最後的結果與真實值差距越小越好。
在 Neural Network 我們要訓練的變數就是前面一篇提到的 weight 和 bias。一開始我們隨機的給予這些數字,然後在一次次的學習中去改進 weight 和 bias 的值,找到最小的成本函數。
在課程的例子裡,Neural Network function 的 input 是 784 個 pixel 的數字,output 是 10 個數字,0 到 9 的機率,parameters 是 weight 和 bias。但在cost function 中,weight 和 bias 變成了 input,而 output 就是 cost 的值,parameters 則是很多的 training pairs。
我們可以把 cost function 這樣表示,
\[C(w_1, w_2,..., b_1, b_2, ....) = cost\]cost 的算法是 Neural Network 算出來的值,扣掉正確值然後平方相加。學習過程中,我們將所有 training data 的 cost 相加平均(average cost of all training data),希望這個值越小越好。
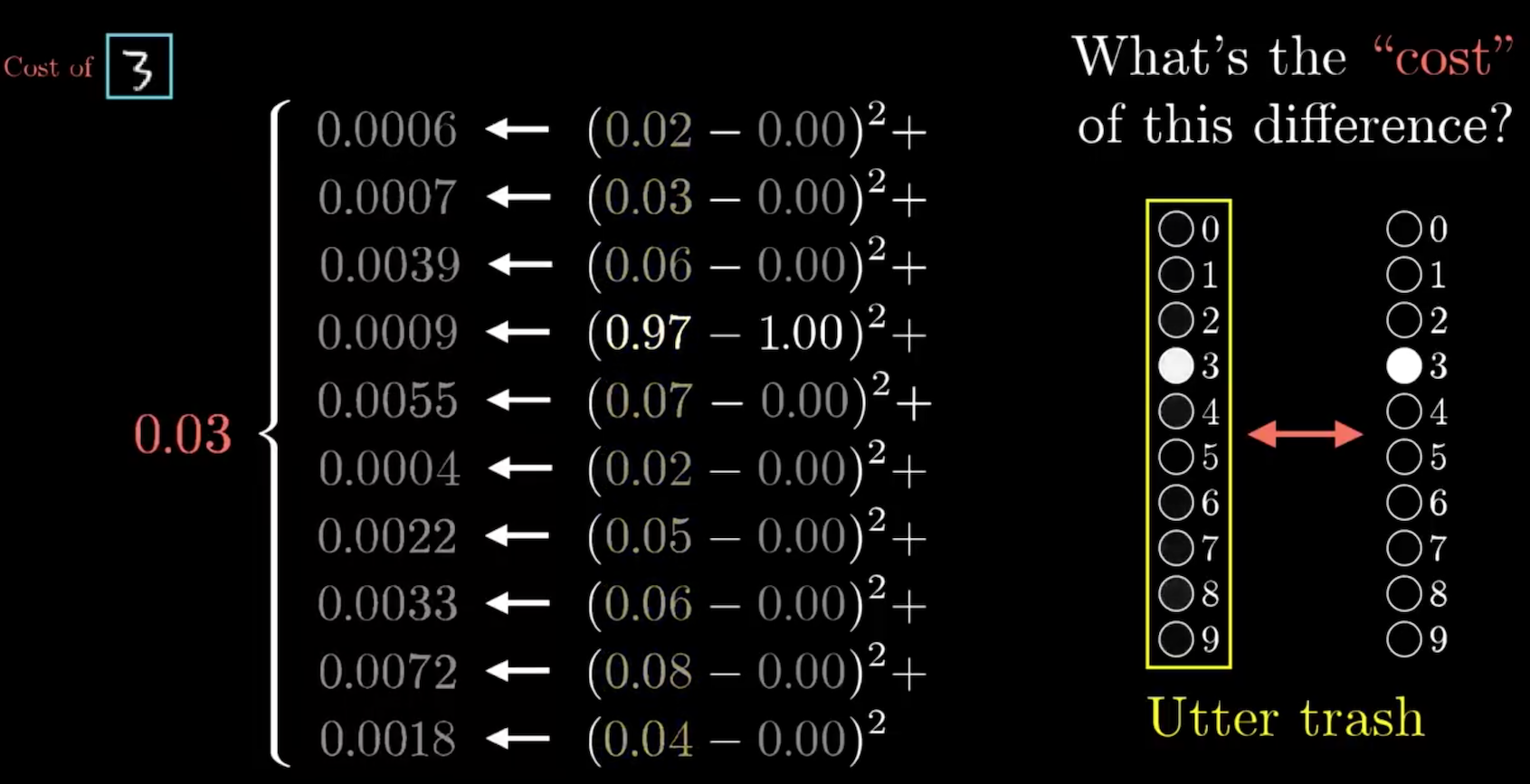
那我們要如何找到最小的 cost 值?
如果 cost function 是一個像下圖的函數圖形,我們知道微分等於 0 可以找到最小值,但這並非一件容易的事,尤其是當我們有很多變數時。
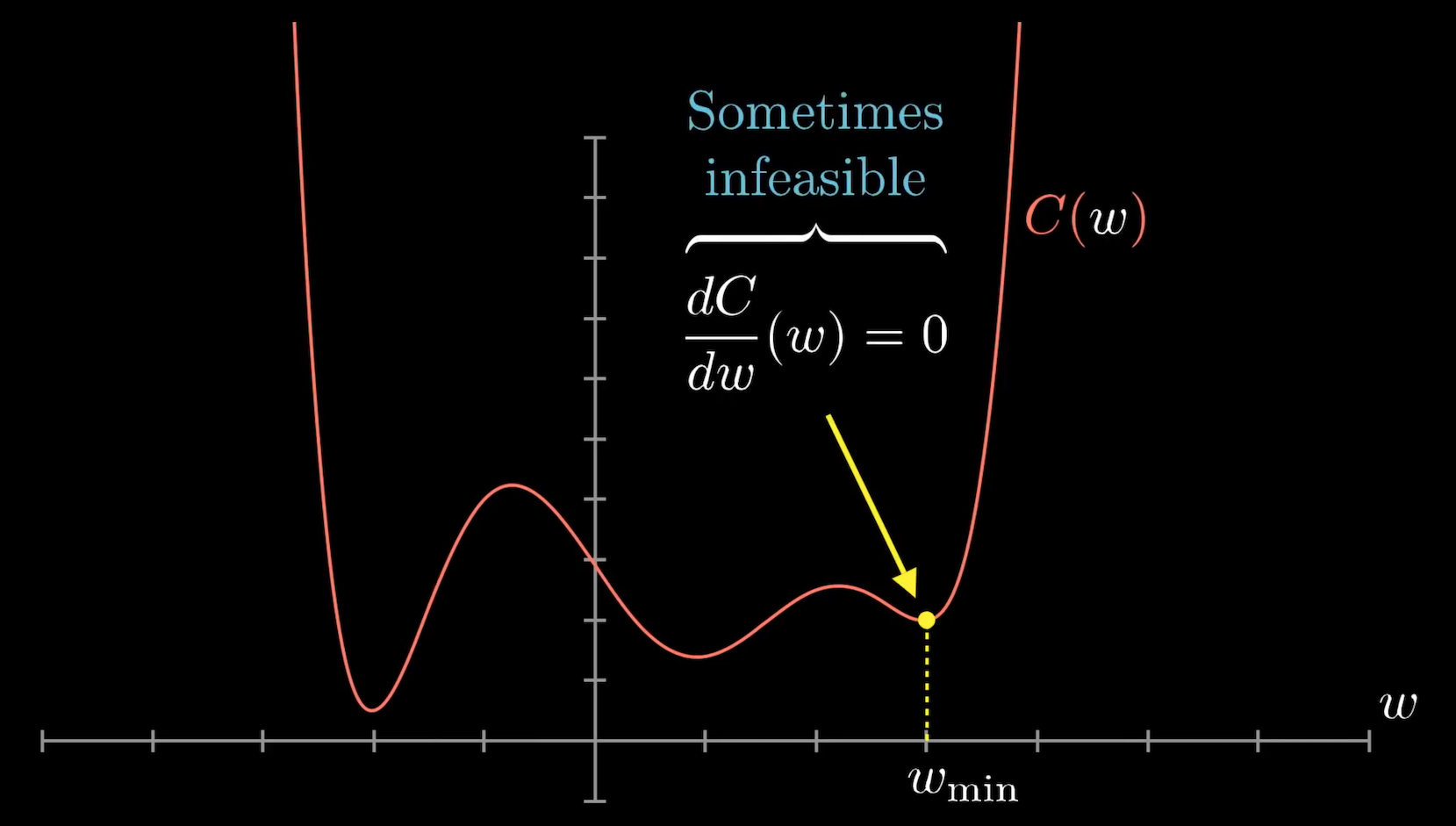
所以我們可以用的方法是,先隨機到函數圖形上的一點,然後根據該點的切線斜率來決定該往哪個方向移動可以找到最低點。這樣的方法,可以讓我們到 local minimum,我們無法確認找到的最小是否是 global minimum,因為這取決與一開始的 initial value。
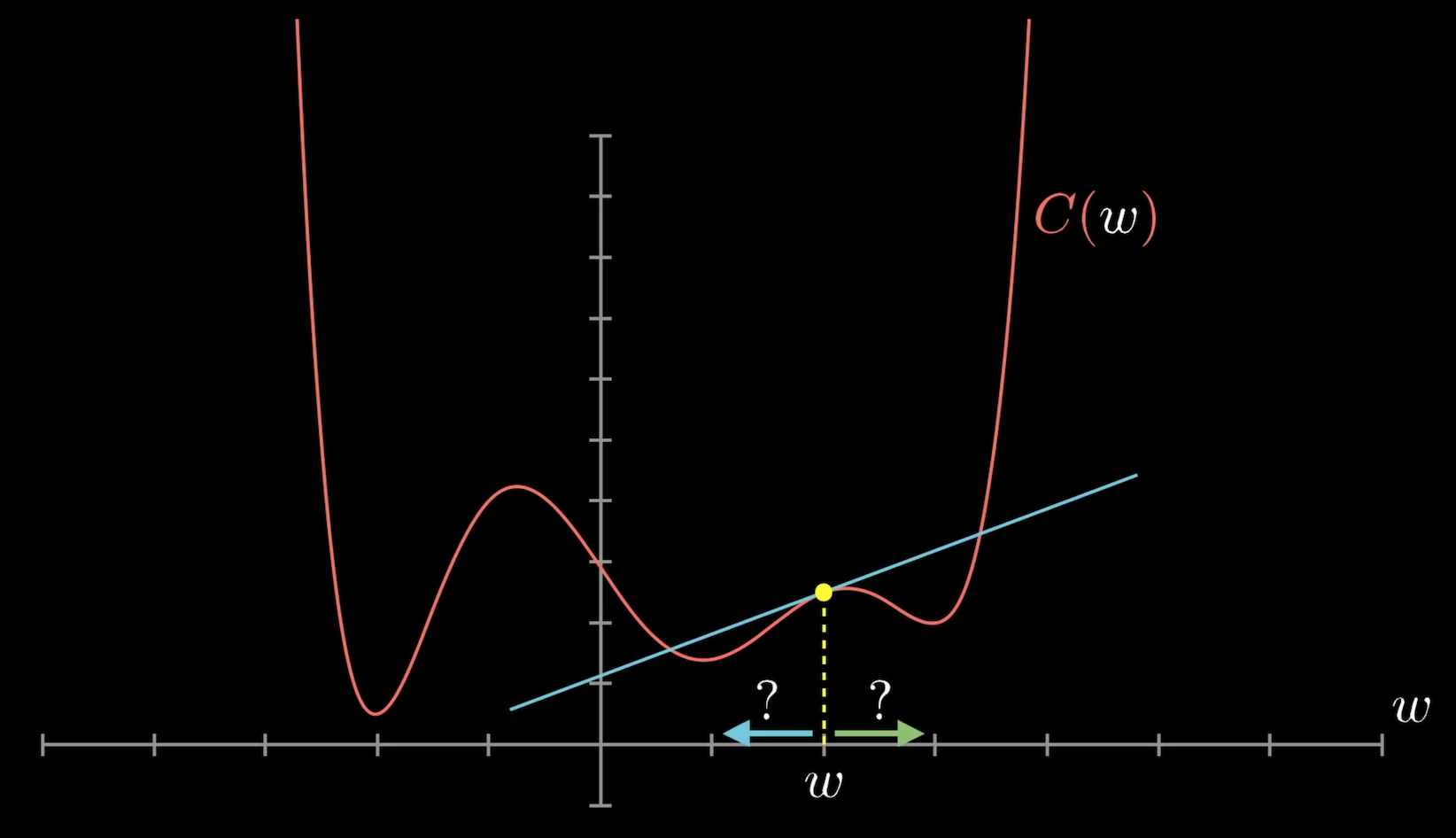
在進入 Gradient descent 之前,我想要先介紹一下基礎觀念。以下將會講解,
- 導函數 Derivative function 與導數 Derivative
- 方向導數 Directional derivative
- 偏導數 Partial derivative
- 梯度 Gradient
導數 Derivative
切線的斜率稱為「導數」(Derivative),也就是微分。
定義成,
\[m = \text{lim}_{\Delta x \to 0}\frac{f(x+\Delta x) - f(x) }{\Delta x} = f'(x) = \frac{\text{d} f(x)}{\text{d}x}\]偏導數 Partial derivative
斜率求的是單變數的微分,而偏導數是在多變數中的某個變數方向的斜率。
以兩個自變數為例, \(z = f(x, y)\)
\(f_x(a, b)\) 為對 \(x\) 的偏導數,定義為
\[f_x(a, b) = \text{lim}_{h \to 0} \frac{f(a + h, b) - f(a, b)}{h}\]\(f_y(a, b)\) 為對 \(y\) 的偏導數,定義為
\[f_y(a, b) = \text{lim}_{k \to 0} \frac{f(a, b + k) - f(a, b)}{k}\]也就是對 x 或 y 方向做偏微分。
方向導數 Directional derivative
斜率求的是單變數的微分,在多變數中要求斜率必須要看是哪個方向的斜率,因為各個方向的斜率都不相同,這時要求的就是方向導數。
假設函數 \(z = f(x, y)\),在定義域 \(xy\) 平面上有一點 \((x, y)\) 及單位向量 \(\overset{\rightharpoonup}{u} = (u_1, u_2)\)。則曲面 \(z = f(x, y)\) 在 \((a, b)\) 處,沿 \(\overset{\rightharpoonup}{u}\) 的方向的斜率定義為,
\[\text{D}_u f(x_0, y_0)= \text{lim}_{h \to 0} \frac{f(x_0 + h u_1, y_0 + h u_2) - f(x_0, y_0)}{h} = \nabla f \boldsymbol{u}\]方向導數的意義在於,有助於計算出空間中某一場量 \(f(x, y, z)\) 在某一特定方向 \(\boldsymbol{u}\) 之變化率。
梯度 Gradient
梯度的定義就是對各個分量做偏微分。
例如,現在是兩變數函數 \(f(x, y)\),其梯度 \(\nabla f(x, y)\) 定義為
\[\nabla f(x, y) = \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right)\]若是變數有三個,則 \(\nabla f(x, y, y)\) 定義為
\[\nabla f(x, y, z) = \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\right)\]Gernal 來看,有 n 個變數的函數 \(f(x_1, x_2, \cdots, x_n)\),我們可以寫成
\[\nabla f(x_1, x_2, \cdots, x_n) = \left(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \cdots, \frac{\partial f}{\partial x_n}\right)\]梯度 Gradient 的幾何意義,
- \(\nabla f\) 表示曲面 \(f(x, y, z) = C\) 之垂直向量,如下圖所示。
- \(\nabla f(P)\) 表在 \(P\) 點增量最大的方向,也就是 the direction of steepest increase
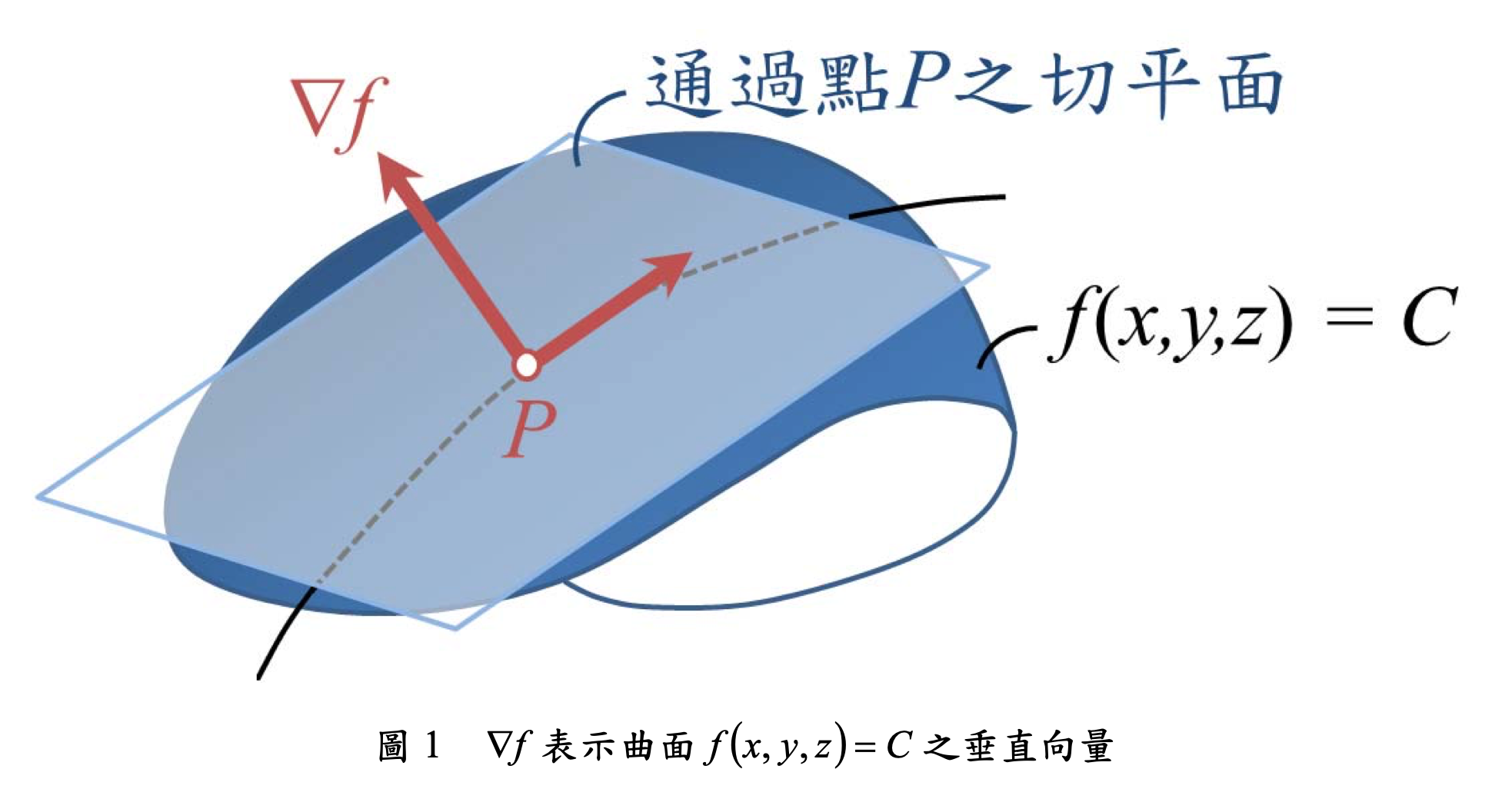
梯度下降法 Gradient descent
Gradient descent 是一種最佳化方法。
從上一部分,我們知道 P 點 gradeint 表示該點增量最大的方向。現在我們要找 cost function 的最小值,也就是該 function 斜率為 0 的點,當我們今天在 P 點知道哪個方向是會增加最快速的點,那就只要往反方向就會是減少最快速的方向了。也就是 \(-\nabla f(P)\) 是找尋 minimum cost 的方向。
總的來說,梯度下降法 Gradient descent 就是不斷的在某個點 P 算它的 Gradient,然後往 Gradient 的反方向一定,直到找到 local minimum 為止(無法知道是否找到 glocal minimum,會根據 initial values 而定)。
在 neural netword 中,讓這個梯度計算更有效率的方法叫做 Backpropagation,而這正是 neural netword 的重點!下一篇繼續介紹 :)
Reference:
方向導數(Directional Derivative)之定義與意義
純量函數之梯度(Gradient)
