This post is based on the 732A92 Texting Mining course, given by Marco Kuhlmann at LiU in 2019.

這門課教授的是英文的文字探勘，中文與英文本身在結構上有非常大的差異，所以有些解析和斷詞的方法中文可能並不適用，但在基本概念上還是有相同的地方。

每個主題都有一個 Lab 附在文章最後。

Information Retrieval (IR)

Information Retrieval (IR) is finding material (usually documents) of an unstructured nature (usually text) that satisfies an information need from within large collections (usually stored on computers).

中文稱為「資訊檢索」。從一堆的 unstructured 資料中（通常是文字）找出符合我們需要的條件的資料。

例如，google 搜尋就是一個例子。我們在搜尋 bar 裡輸入我們想要找到的關鍵字，google 搜尋引擎會從它儲存的所有 database（網站們） 中找出符合我們關鍵字條件的網站給我們。

那我們要如何找到包含這些關鍵字的文章呢？

最直觀地想應該就是把有我們搜尋的關鍵字的文章抓出來吧！這就是 Boolean retrieval。

在進入 Boolean retrieval 之前先來看一下 The classic search model。

The classic search model

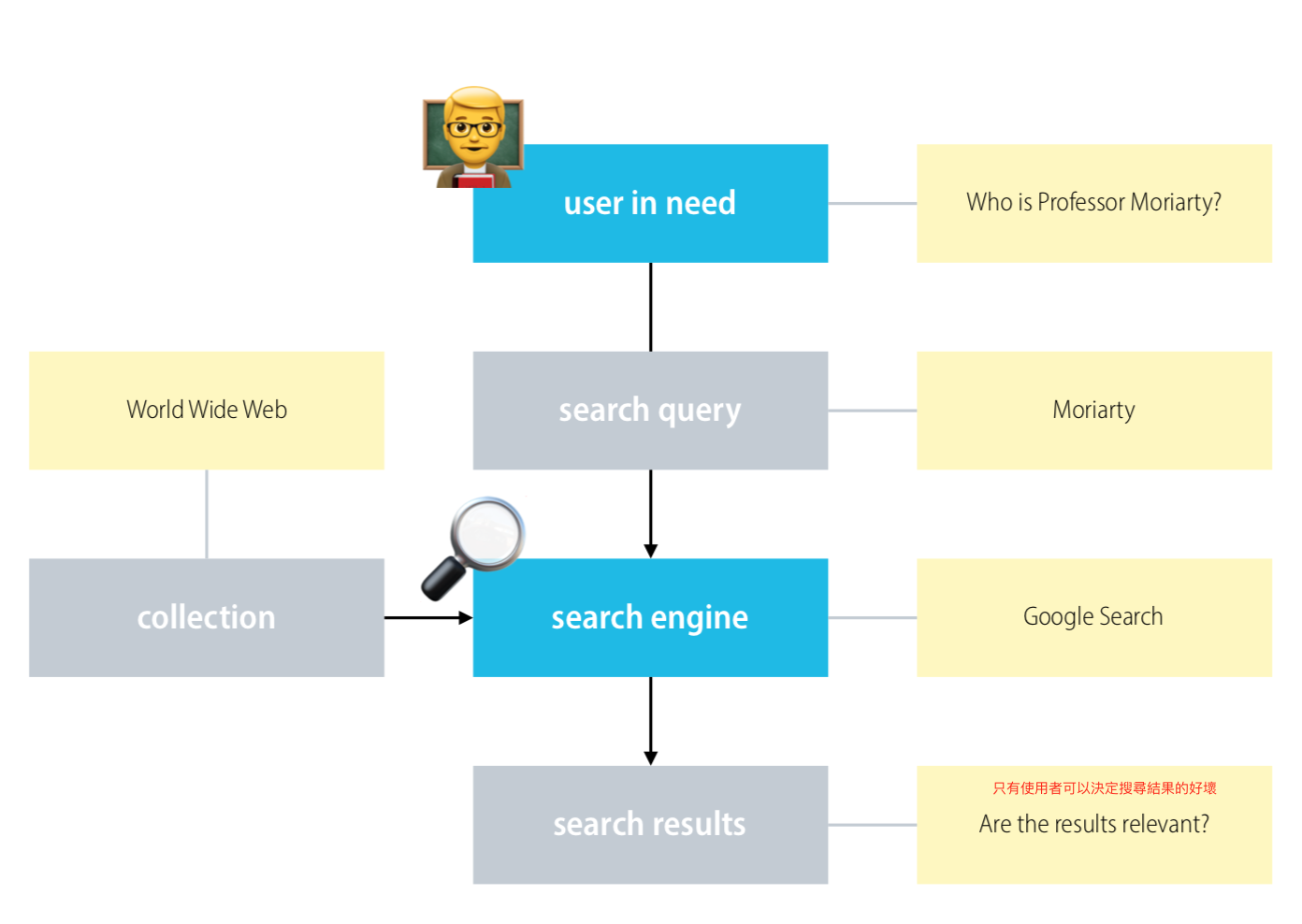
• To communicate her/his information need to an IR system, the user formulates a search query.
• The objective of the IR system is to find documents in the collection that ‘match’ the search query.
• A good IR system finds documents that are also relevant for the user’s information need.

Boolean retrieval

The Boolean retrieval model is a model for information retrieval in which we can pose any query which is in the form of a Boolean expression of terms, that is, in which terms are combined with the operators AND, OR, and NOT. The model views each document as just a set of words.

很直覺的方法要找出包含關鍵字的可以使用 terms(通常是個單詞) 是否包含在 documents 裡。

例如，現在有 Sherlock Holmes 小說文字。我想要找出哪些篇章符合出現 ‘Moriarty’ 和 ‘Lestrade’ 但不包含 ‘Adair’。那麼下的 query 就會是 Moriarty AND Lestrade AND NOT Adair

那個我們可以將上面的概念寫成一個 Term–document matrix。

Term–document matrix

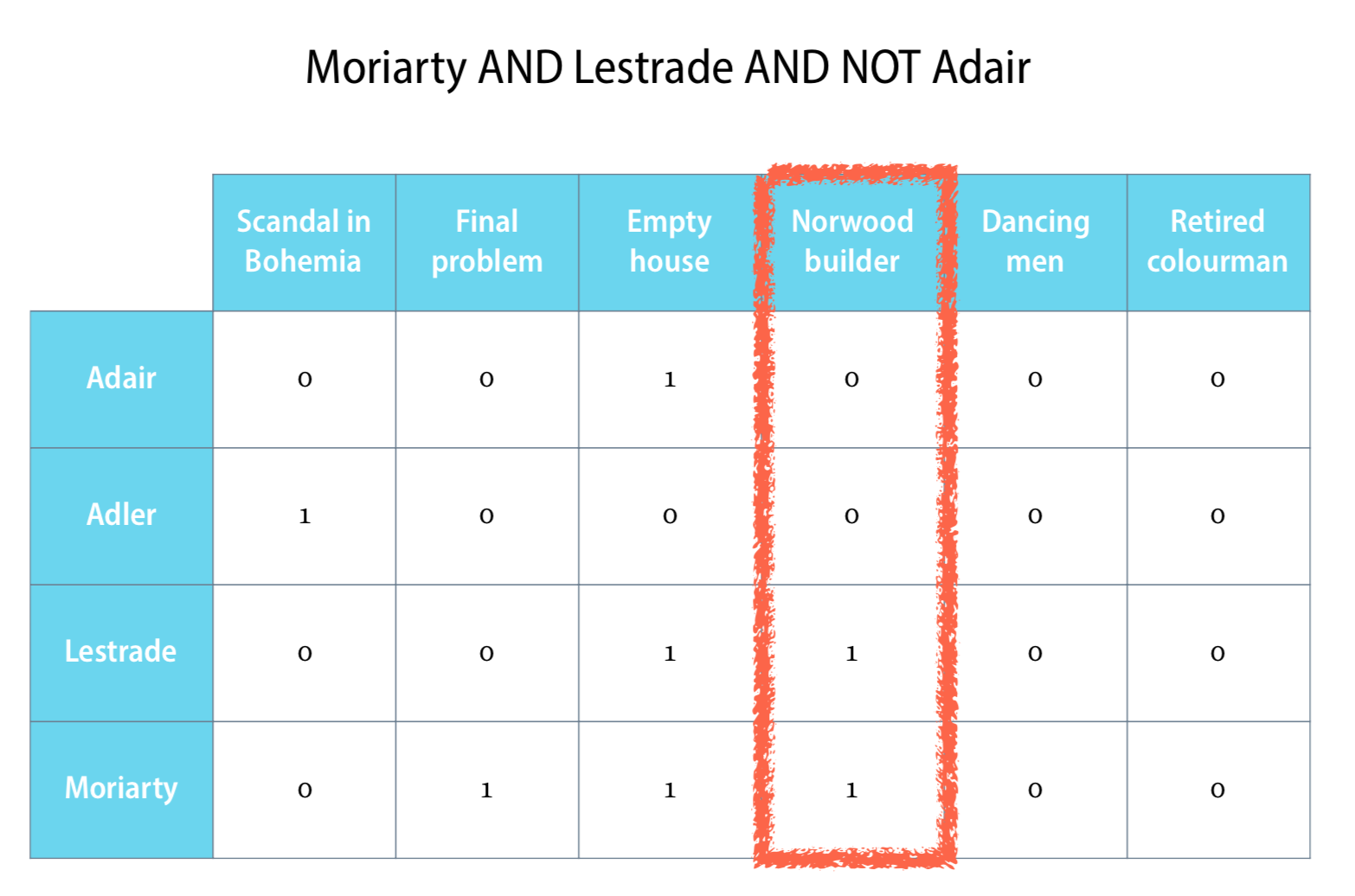
每一行代表一個章節，每一列代表一個條件的單詞（term）。以列來看，0 表示該單詞沒有出現在那一章節中，1 表示該單詞有出現。
像是第一列，’Adair’ 只有出現在 ‘Empty house’ 這個章節。

這樣的方法看似簡單，但以實務上來說並不是個好辦法。因為，

• Term–document matrices are sparse. 可以從上面的 matrix 看到，有很多的 0 ，也就是說其實很多資訊並不需要，但卻還是需要儲存。
• 假如現在有 1,000,000 份 documents，有 500,000 不同的 terms ，這樣的條件下會產生 a matrix with 500,000,000,000 entries (62,5 GB)。

所以我們必須得使用別的辦法減少不必要的資訊儲存。這時候就有了 Inverted index。

Inverted index

The inverted index is a key–value mapping, the basic idea is shown below.

• the keys are search terms
• the values are sorted lists of document identifiers (ids)
• the list for terms identifies those documents that contain the terms

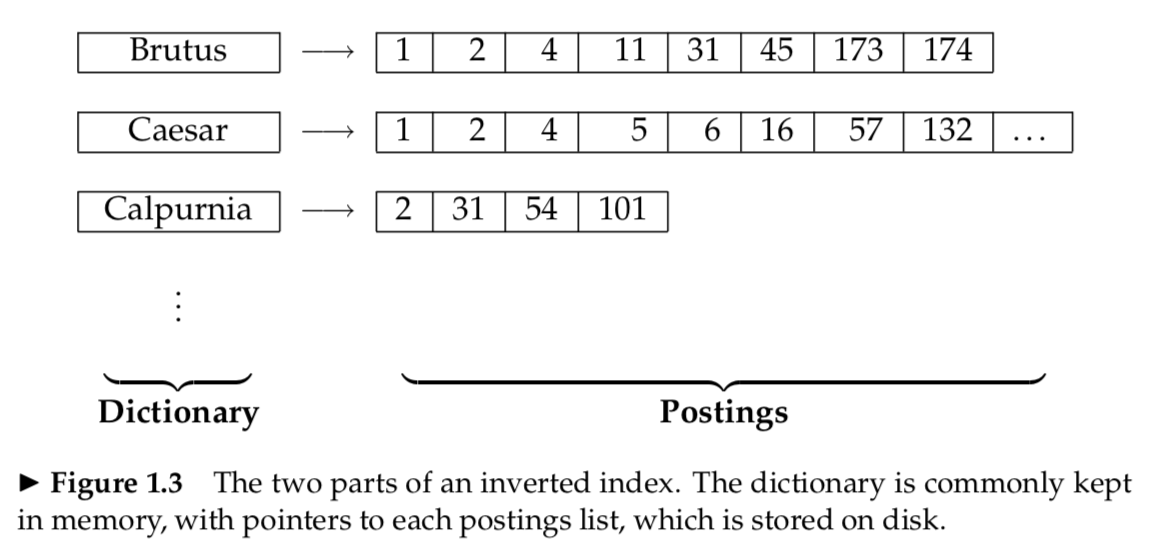
從上圖我們可以看到，和 Term–document matrix 不一樣的是 Inverted index 只儲存了有包含該單詞的 document ids。

現在我們知道我們要的是去看那些關鍵字是否包含在 documents 中，但我們並不會每一次找關鍵字的時候一篇一篇文章搜索，我們會先建立一個儲存好所有 term 的 matrix， 但我們要怎麼決定是哪些 terms 要被儲存呢？

Index construction

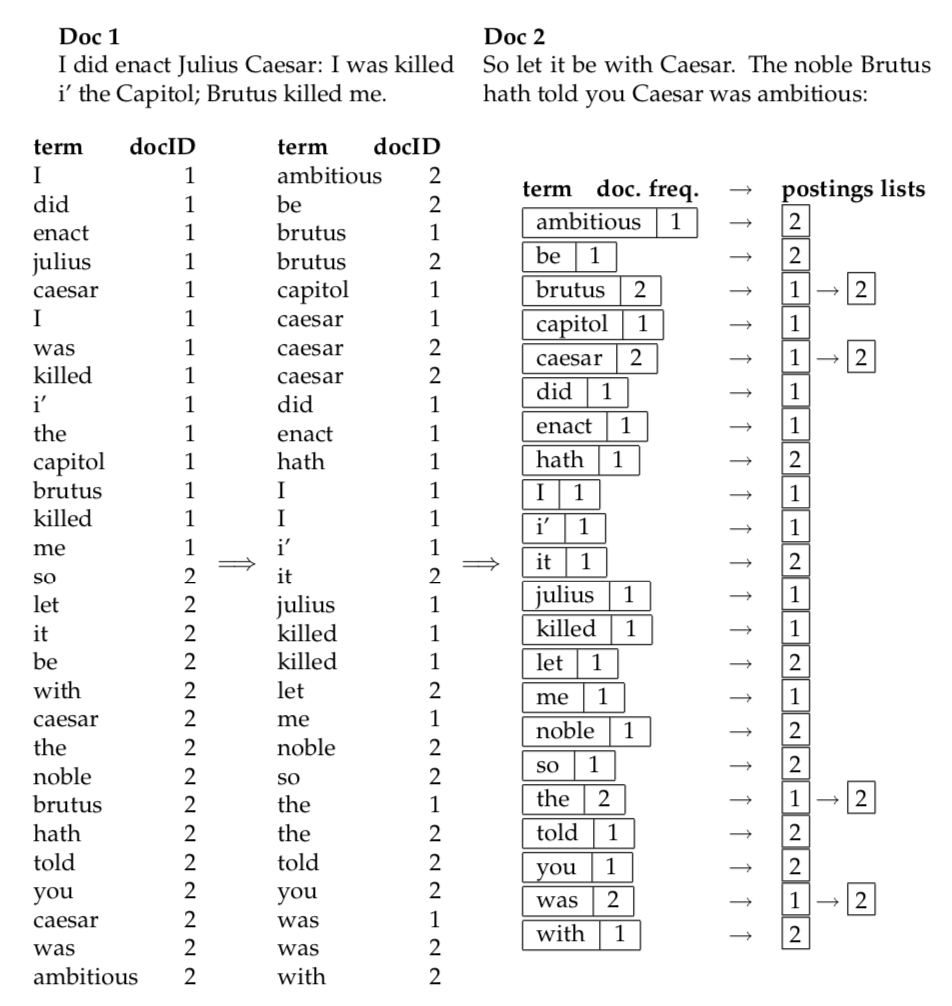
The major steps in index construction:

1. Collect the documents to be indexed.
2. Tokenize the text.
3. Do linguistic preprocessing of tokens.
4. Index the documents that each term occurs in.

Tokenization

raw = "Apple is looking at buying U.K. startup for $1 billion."
# tokenize raw text based on whitespace
for token in raw.split(): 
	print(token)


# tokenize using spaCy
import spacy

nlp = spacy.load("en_core_web_sm") 
for token in nlp(raw):
    print(token.text)

# 結果：
# Apple
# is
# looking
# at
# buying
# U.K.
# startup
# for
# $
# 1
# billion
# . 

英文每個單字可以很容易地使用空白（.split()）來分割出每個單字，但只使用 split 無法排除標點符號的問題，python 的 spacy 可以將標點符號也區分出來。

Stop words

A stop word is a word that is frequent but does not contribute much value for the application in question. For example: a, the, and…

但根據分析的目的不同，會有不同的 stop words 的定義。以分析 Sherlock Holmes 的小說為例，資料裡面肯定會包含非常大量的 Sherlock Holmes，那這種時候我們或許可以根據分析的目的將 Sherlock Holmes 定義為 stop words。換句話說，並不存在一個所有分析通用的 stop words 資料集。

既然 stop words 對於分析沒有價值貢獻，那麼在做分析前就必須把 stop words 刪除，以避免干擾分析結果。

Lexemes and lemmas

英文的文法有幾個規則，

1. 動詞會根據人稱與時態有所變化
2. 動詞有動名詞型態
3. 名詞的單數與複數有變化

但在分析前必須要將這些相同意義但不同型的單字修正為相同以便分析。

• The term lexeme refers to a set of word forms that all share the same fundamental meaning.
  For example: word forms run, runs, ran, running – lexeme run

• The term lemma refers to the particular word form that is chosen, by convention, to represent a given lexeme.
  For example: what you would put into a lexicon

Ranked retrieval（排序檢索）

進行到這裡我們已經知道如何要先建立一個有所有 term 的 matrix for 所有的 documents，然後使用 boolean retrieval 找出我們要的 documents，但這樣並沒有考慮到單詞的重要性。換句話說，一個很常出現的單詞有可能並沒有比一個出現次數較少但卻在某 document 出現還要重要，我們可能更想要抓出含有那個單詞的文章。所以我們必須要 rank 那些抓出來的 terms。

Problems with Boolean retrieval

• Not many users are capable of writing high-quality Boolean queries, and many find the process too time-consuming.
• Feast or famine: Boolean queries tend to return either too many results, or no results at all.
• Intuitively, whether or not a document ‘matches’ a search query is not a Boolean property, but is gradual in nature.

Ranked retrieval

• A ranked retrieval system assigns scores to documents based on how well they match a given search query. (There are many possible ways of scoring.)

• Based on the score, a ranked retrieval system can return a list of the top documents in the collection with respect to the query.

前面提到的 boolean retrieval 只考慮了文件是否包含或不包含要的詞彙，為了那個詞彙的「重要性」也考慮進去，我們要給予每個 term 不同的 weight。

Term weighting

• The score of a document d with respect to a query q is the sum of the weights of all terms t that occur in both d and q.

• Any specific way to assign weights to terms is called a term weighting scheme.

計算 weight 的方法有很多種，也可以自行定義，這邊介紹一種常用的方法。

TD–IDF weight

TD–IDF is Term frequency–inverse document frequency. This formula includes two parts: Term frequency & Inverse document frequency.

Term frequency

The number of times a term t occurs in a document d is called the term frequency of t in d, and is denoted by tf(t, d).

-A problem with term frequency

Relevance is not a linear function of term frequency. 例如，一個出現20次的單詞難道就代表它比一個只出現1次的單詞重要20倍嗎？為了要降低出現頻率造成太大的影響，所以我們將 frequency 取 log，這時候 weight(t, d) 定義成，

稱作，log-frequency weighting

-Another problem with term frequency

時常重複出現的慣用詞彙對一個文件的影響很大。例如，現在想要考慮 Sherlock Holmes 裡包含 Moriarty 和 Holmes 的章節，但當我們下 query 去找時會發現，Holmes 出現最多的章節幾乎沒有 Moriarty，這是因為 Holmes 在這些文本裡出現的比例實在太高了，如果直接以它出現的頻率來分析肯定會造成很大的誤差，進而影響了出現次數少很多的 Moriarty。所以這時候 Inverse document frequency 就非常重要了！

Inverse document frequency

• Let N be the total number of documents in the collection.
• The number of documents that contain a term t is called the document frequency of t, and is denoted by df(t).

It denotes by idf(t):

df(t) 越大代表該詞彙出現在越多文章中，也就是說，如果 df(t) 越常出現，則 idf(t) 就會越小，換句話說，該詞彙的重要性越小。

TD–IDF Weight

現在我們有了 td 和 idf，tf–idf weight 就是將這兩個數字相乘（出現次數乘以重要性），

The tf–idf weight of a term t in a document d is defined as

where N denotes the number of documents in the collection.

Variations of the tf–idf weighting scheme

因為 df(t) 可能是 0，所以我們改良一下上面的式子。

In scikit-learn, the tf–idf weight is computed as

where N denotes the number of documents in the collection.

The vector space model

Document representations

• Documents as sets of terms
  In Boolean retrieval, the only relevant information is whether or not a term is present in a document.

• Documents as bags of terms
  In ranked retrieval based on term frequency, the only relevant information is how often a term is present in a document.

The vector space model – idea 1

Represent documents as vectors in a high-dimensional space:

• The dimensions (axes) of the space correspond to the terms in the vocabulary (potentially relevant terms). For example: could be set of all words in the collection, set of most frequent words, …
• The values of the vector components depend on the term weighting scheme: Boolean values, counts, tf–idf values, … (in scikit-learn: CountVectorizer, TfidfVectorizer)

The vector space model – idea 2

To rank documents in the vector space model,

• we represent the query as a vector in the same space as the documents in the collection
• we compute the score of a candidate document as the similarity between its document vector and the query vector (similarity = proximity in the vector space)

Cosine similarity

以下舉一個從一篇部落格看到的例子，

例如: Query = {“Hello”} Doc1 = {“Foo”, “Foo”} Doc2 = {“Hello”, “World”}

在經過計算之後，我們知道其向量分別為（可以使用 tf-idf values, counts,… 等等）

Query = (1, 0, 0) Doc1 = (0, 0, 2) Doc2 = (1, 1, 0)

我們可以使用歐幾里德距離算出 query 和兩個 documents 的距離分別是，根號5和1。但計算歐幾里德距離忽略掉了單詞出現的頻率的影響。

如果說今天把上面的向量改一下，

Query = (2, 0, 0) Doc1 = (0, 0, 4) Doc2 = (2, 2, 0)

這時候 所有的距離都變成了兩倍，但其實他們完全是平行的向量。

那如果我們考慮向量之間的角度呢？也就是計算兩個向量的 dot，這時候會發現，長度還是影響了最後的數值。

因此，使用 Cosine similarity 來將數值 normalized。使用 cosine 後，數值只會介於 -1 和 1 之間，並且只需要考慮非0的數值。

Evaluation of information retrieval systems

To evaluate an IR system we need:

• a document collection
• a collection of queries
• a gold-standard relevance judgement

Precision:

Precision (P) is the fraction of retrieved documents that are relevant

Recall:

Recall (R) is the fraction of relevant documents that are retrieved

F1-measure

A good system should balance between precision and recall. 

The F1-measure is the harmonic mean of the two values:

Lab: Information Retrieval Lab

Reference:
732A92 Texting Mining
Introduction to Information Retrieval
[文件探勘] TF-IDF 演算法：快速計算單字與文章的關聯
Vector Space Model(1)
如何辨別機器學習模型的好壞？秒懂Confusion Matrix