前面介紹了 Convolution operation。

• Padding
• Strided Convolution
• Convolutions Over Volume ***

Padding

為什麼需要 Padding?

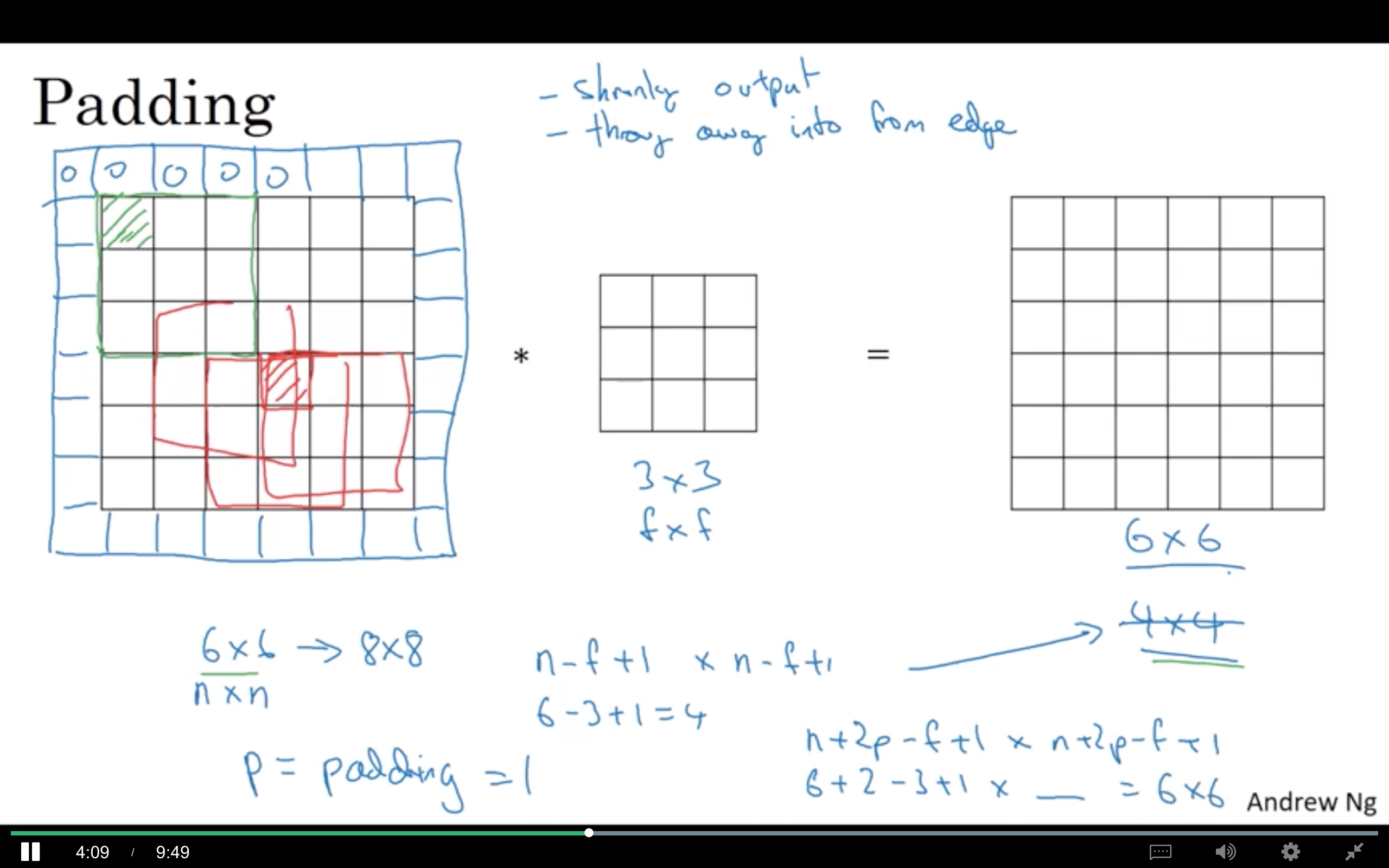
Convolution operation 的缺點：

1. 經過 convolution fitler 後原始圖將變小。如果有很多層 convolutional layer，資訊在每次運算後不斷損失。
2. 最邊緣的 pixel 只會被使用到一次，但中間的 pixel 會使用到較多次。也就是說，會有邊緣的很多資訊缺失。

所以為了解決以上的缺點，我們將 input 的圖的邊緣加上一個 pixel，這樣經過卷積運算後的圖像仍和原圖一樣大。邊緣也是可以加 2 pixel 的。

以上圖為例，原本為 6x6(nxn) 的圖，經過 3x3(fxf) 的 filter 做卷積運算後，變為 (n-f+1)x(n-f+1) 的圖。

但如果今天邊緣加上 p pixel，最後圖檔就會變為 (n+2p-f+1)x(n+2p-f+1) 的圖。

---

The choice of padding - Vaild and Same convolutions

1. Vaild - No padding
2. Same - Pad so that output size is the same as the input size
   根據上面的公式，如果在 input 圖邊緣加上 pixel 後經過卷積運算要和原始圖檔大小ㄧ樣，那要符合 n+2p-f+1 = n，那就會得到 p = (f-1)/2

For computer vision, usually f is odd. 3 by 3 filters are very common.

---

Strided Convolution

前面我們在做 convolution 時 filter 都是一次跳一格計算，strided 則是一次跳不只一格。

如下圖，這時候最後結果的 pixel 也會不同，計算公式就會是 ((n+2p-f)/2)+1 取 floor。

---

cross-correlation vs. convolution

• cross-correlation：數學家喜歡將 convolutional operation 稱為 cross-correlation。在做運算時會將 filter 做水平與垂直翻轉，如下圖。
• convolution：在 deep learning 通常都稱為 convolution，且不會將 filter 做鏡射的動作。

那這樣幹嘛要翻轉？因為在做訊號處理時，翻轉後會有一些好的特性可以拿來使用。但在做 deep learning 時基本上沒有影響，所以做 deep learning 時不會翻轉 filter。

---

Convolutions Over Volume

Convolutions on RGB impages

前面舉的例子都是在 2D 上計算 convolution，現在要來看如何在 3D 上實現 convolution。

---

Reference:
Coursera - Convolutional Neural Networks(deeplearning.ai)