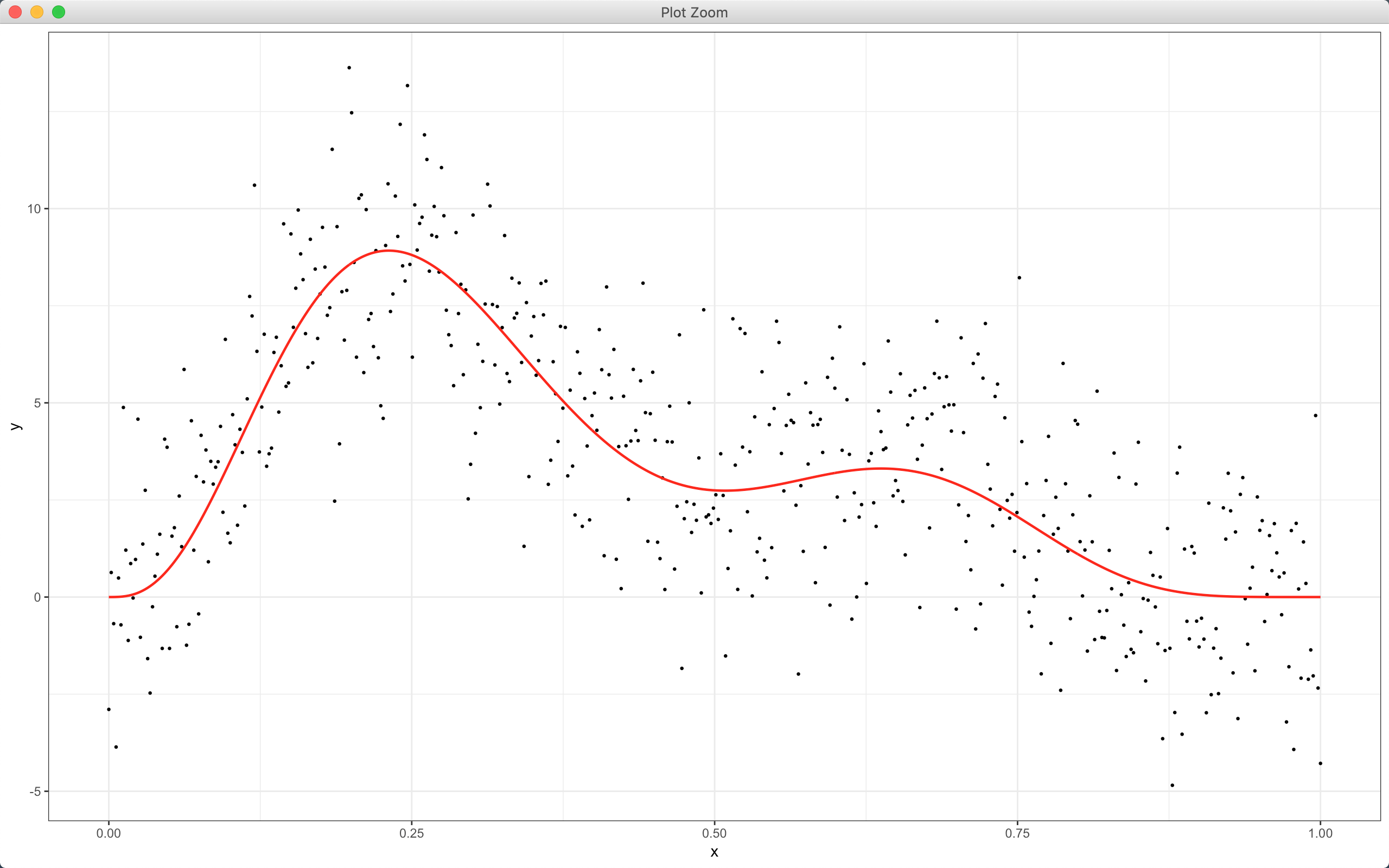
上圖是一個 x, y 的分佈圖，紅線是這些點分部的方程式。但現實中，我們並無法真的知道紅線的方程式，我們可能使用一次方程式、二次方程式甚至更高次方的方程式去嘗試（如下圖 ）。

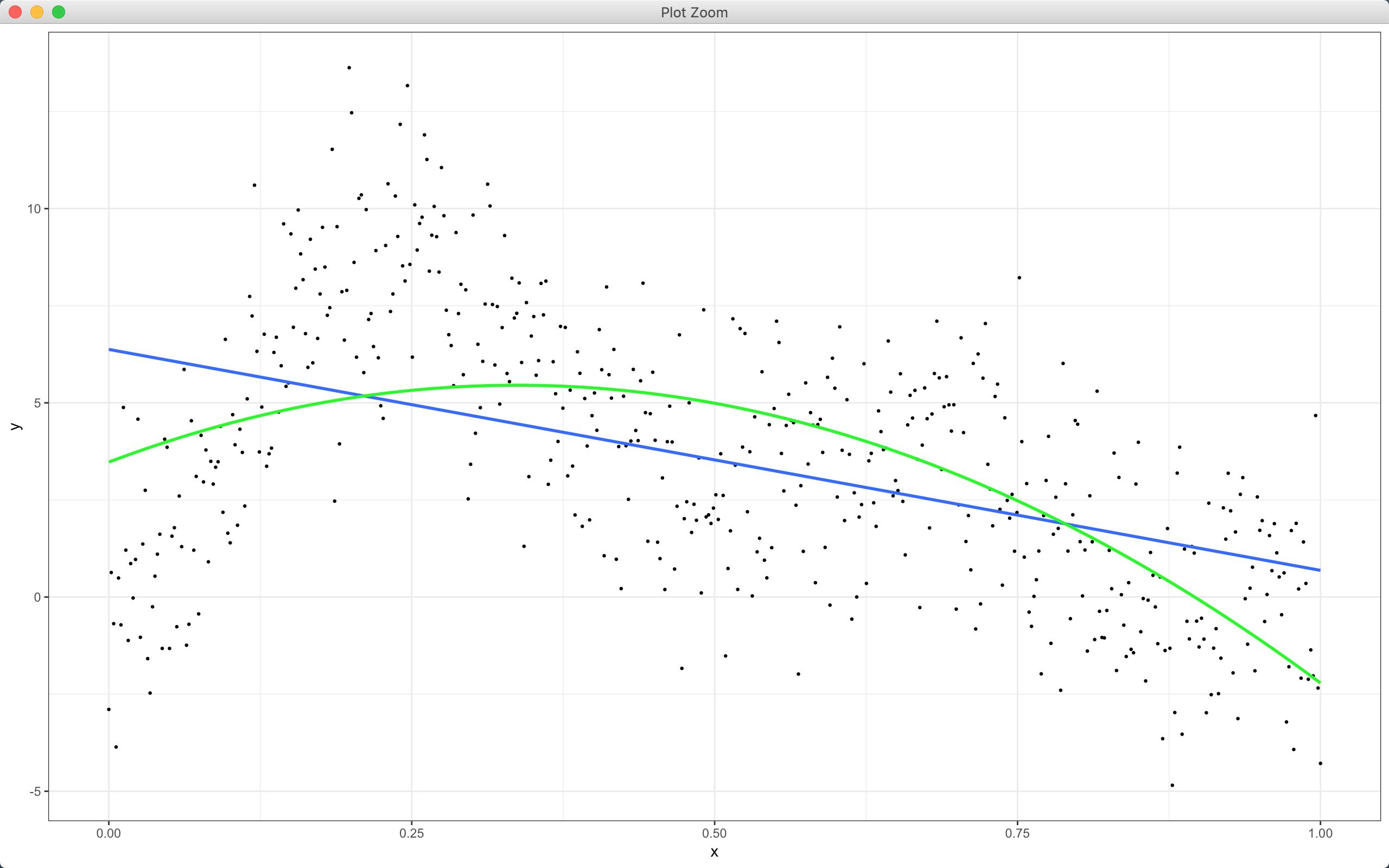
我們可以將擬合的多項式方程式（polynomial function）寫成，

\(y = \beta_0 + \beta_1 x^1 + \beta_2 x^2 + … + \beta_n x^n + \epsilon\)

但只是一味的提高多項式的次方只是增加模型的複雜度會導致 overfitting 的問題，在 testing data 上的結果也不會太好。

這時候我們可以使用 Piecewise 將 data 劃分成多個區間，根據每個區間的 data 給予一個模型去擬合。

Basis function

\(y_i = \beta_0 + \beta_1 b_1(x_i) + \beta_2 b_2(x_i) + … + \beta_n b_n(x_i) + \epsilon_i\)

透過 \(b_1(X)\)、\(b_2(X)\)、……、\(b_n(X)\) 可以將非線性的自變量轉換成線性。

Piecewise Function

將 data 劃分多個區段後，每個區段再各自找到可以擬合的 model，model 可以是一次方程式、二次方程式或是三次方程式等等，不過三次方最常使用。

如下圖每個區段都是用一次方程式去擬合。\(\xi\) 為區段的分隔點，稱為 knot，每個分段函數稱為 piecewise function。

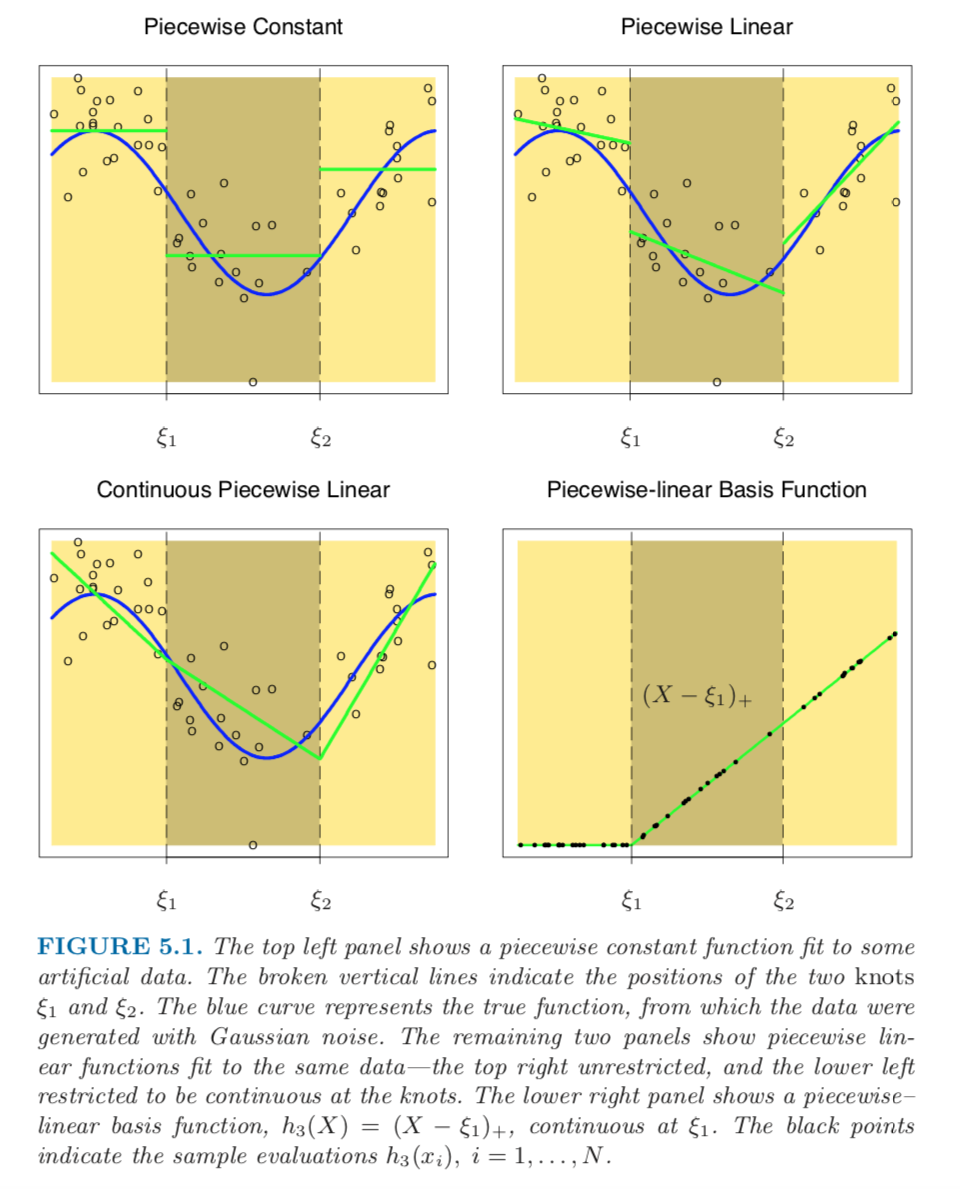From: 《Elements of Statistical Learning》

但這些 piecewise function 是有條件的。
雖然 piecewise function 是每個區段各自擬合出來的 function，但所有區段 function 必須整個為連續，也就是在 \(\xi\) 的交界處的值必須相同。

Cubic Spline

這裡則是使用三次方程式。

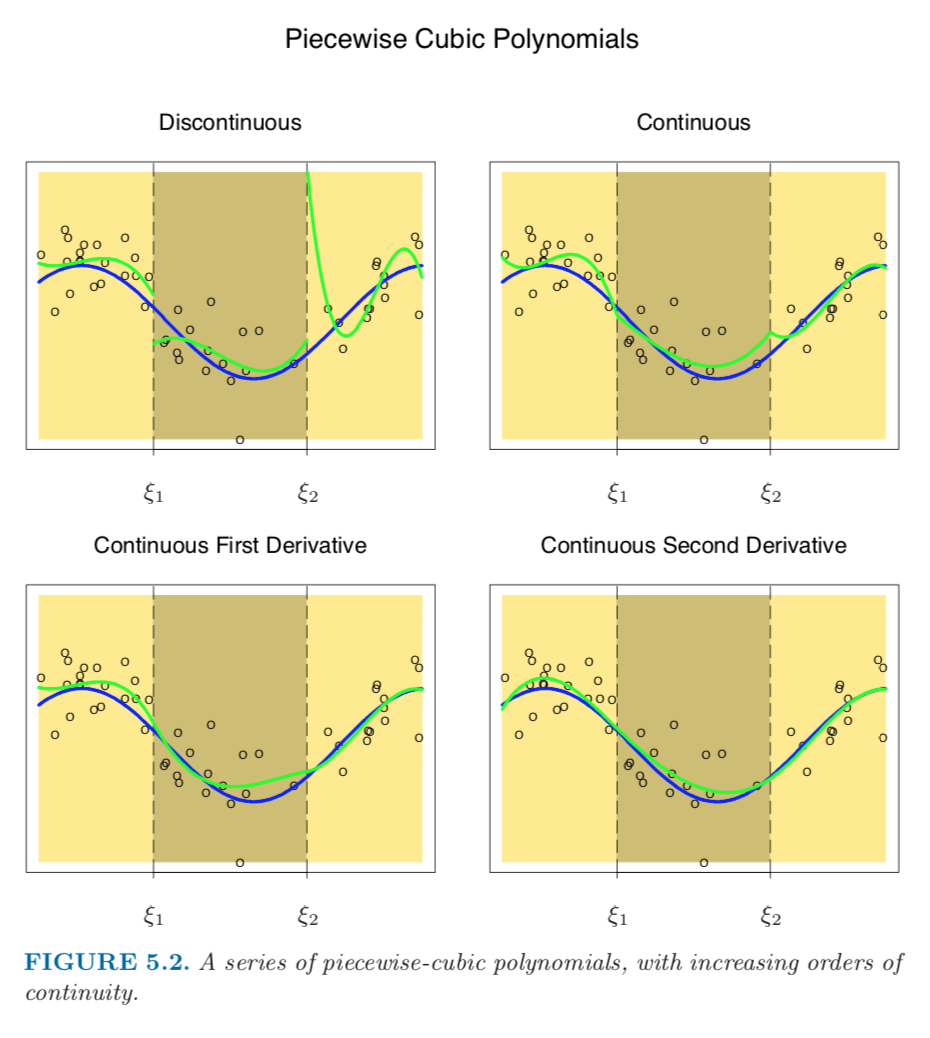From: 《Elements of Statistical Learning》

cubic spline 除了邊界的值相同外，還必須要一階和二階倒數相同。

看上圖左上的圖加上邊界連續後成為右上，雖然看起來是連續的函數，但並不是完美的曲線，如果再加上一階導數相同就變成左下，再加上二階導數就可以畫出右下的圖。

這個 R code 是畫出最上面圖的程式碼，使用 Introduction to Splines 裡頭的範例。

set.seed(100)

# function
f <- function(x) {
  f_x <- 0.2*x^11*(10*(1-x))^6 + 10*(10*x)^3*(1-x)^10
}

x <- seq(from = 0, to = 1, length = 500)
f_x <- f(x)
eps <- rnorm(n = 500, mean = 0, sd = 2) # epsilon
y <- f_x + eps

d <- data.frame(
  x = x,
  f_x = f_x,
  y = y
)

# plot
ggplot(d, aes(x = x)) +
  geom_point(aes(y = y), size = 0.5) + 
  geom_line(aes(y = f_x), colour = "red", size = 0.8) +
  theme_bw()

ggplot(d, aes(x = x, y = y)) +
  geom_point(size = 0.5) + 
  geom_smooth(method = "lm", se = FALSE) +
  stat_smooth(method = "lm", formula = y ~ x + I(x^2), se = FALSE, colour = "green") +
  # stat_smooth(method = "lm", formula = y ~ x + I(x^2) + I(x^3), se = FALSE, colour = "gold1") +
  # stat_smooth(method = 'loess', se = FALSE, colour = "red") +
  theme_bw()

Reference:
一文读懂回归样条（regression splines），附Python代码
Introduction to Splines
Spline Regression | Non Linear Model | Polynomial Regression
wikipedia - 樣條函數
Cubic and Smoothing Splines in R
《An Introduction to Statistical Learning with Applications in R》