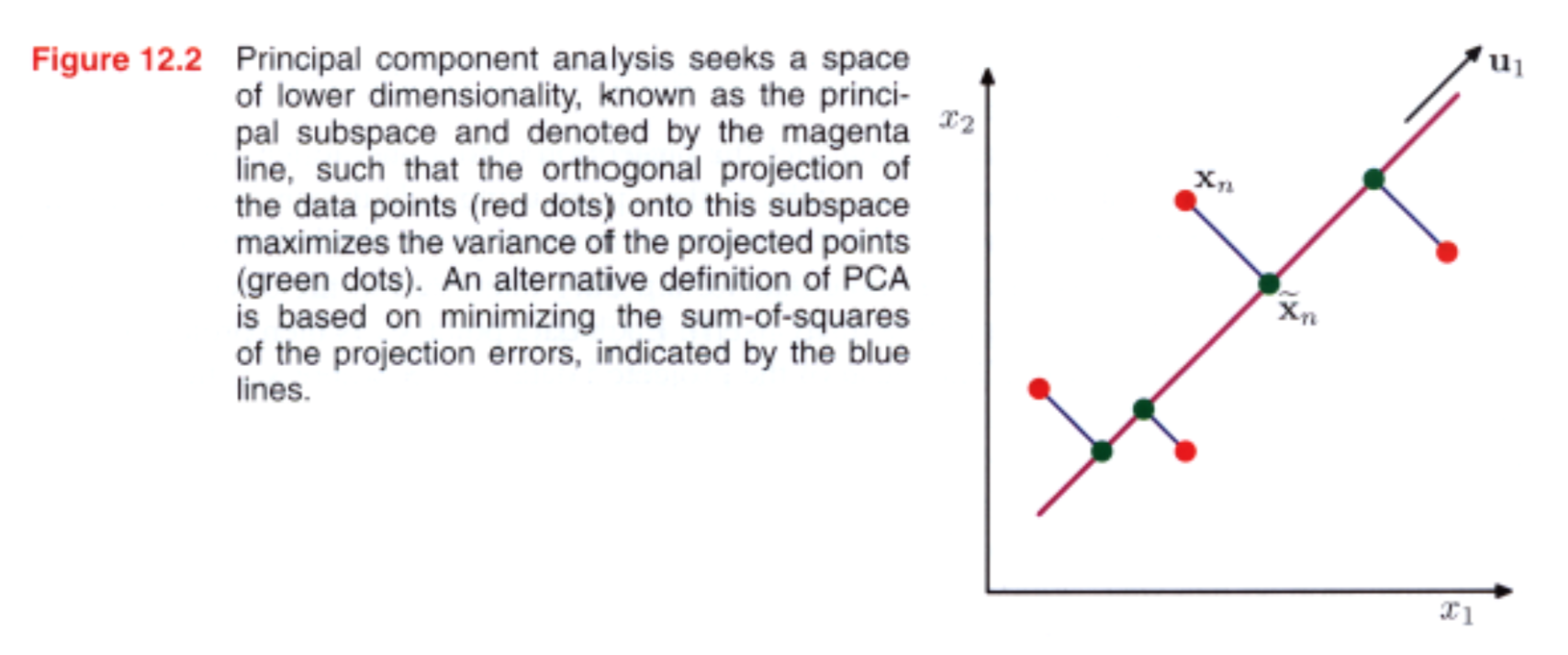
From: «Pattern Recognition and Machine Learning» P.561

---

What is PCA?

Principal Component Analysis(PCA)，中文翻作「主成分分析」。

PCA 是一種將多維度降維的方法。
一個變數其實可能是多個潛在變因（laten variables）組成，但我們無法實際測量出那些 laten variables，而 PCA 就是要拆解出影響較大的變因。使用較少的變數解釋多個 variables。

舉個例子，股市的點數上上下下，我們所能觀測到的是點數這個變數，但其實影響點數變動的潛在變因可能包含了很多市場因素，且每個因素可能又是互相影響。

如果用數學符號表示，\(x_i\) 是我們有的變數，\(z_i\) 是裡頭含有的潛在變因，\(x_i\) 是 \(z_i\) 的線性組合（linear combination）。
\(x_1 = a_{11} z_1 + a_{12} z_2 + a_{13} z_3 + \epsilon_1\)
\(x_2 = a_{21} z_1 + a_{22} z_2 + a_{23} z_3 + \epsilon_2\)
\(x_3 = a_{31} z_1 + a_{32} z_2 + a_{33} z_3 + \epsilon_3\)
……

可以將上式改寫成，
\(z_1 = x_1 u_{i1} + x_2 u_{i2} + x_3 u_{i3}\)
……

---

如何降維？

根據 «Pattern Recognition and Machine Learning» 這本書第 561 頁給了 PCA 兩種定義

1. PCA can be defined as the orthogonal projection of the data onto a lower dimensional linear space, known as the principal subspace, such that the variance of the projected data is maximized (Hotelling, 1933).
2. PCA can be defined as the linear projection that minimizes the average projection cost, defined as the mean squared distance tbtween the data points and their projections (Pearson, 1901).

可以用上圖來理解，或是 StatQuest: Principal Component Analysis (PCA), Step-by-Step 這段。

根據上面的定義，可以看到，降維的方法是要做 orthogonal projection，且找到投影向量讓投影後的資料變異量最大。

這邊我使用 StatQuest: Principal Component Analysis (PCA), Step-by-Step 影片的內容來介紹。

• maximized 什麼？

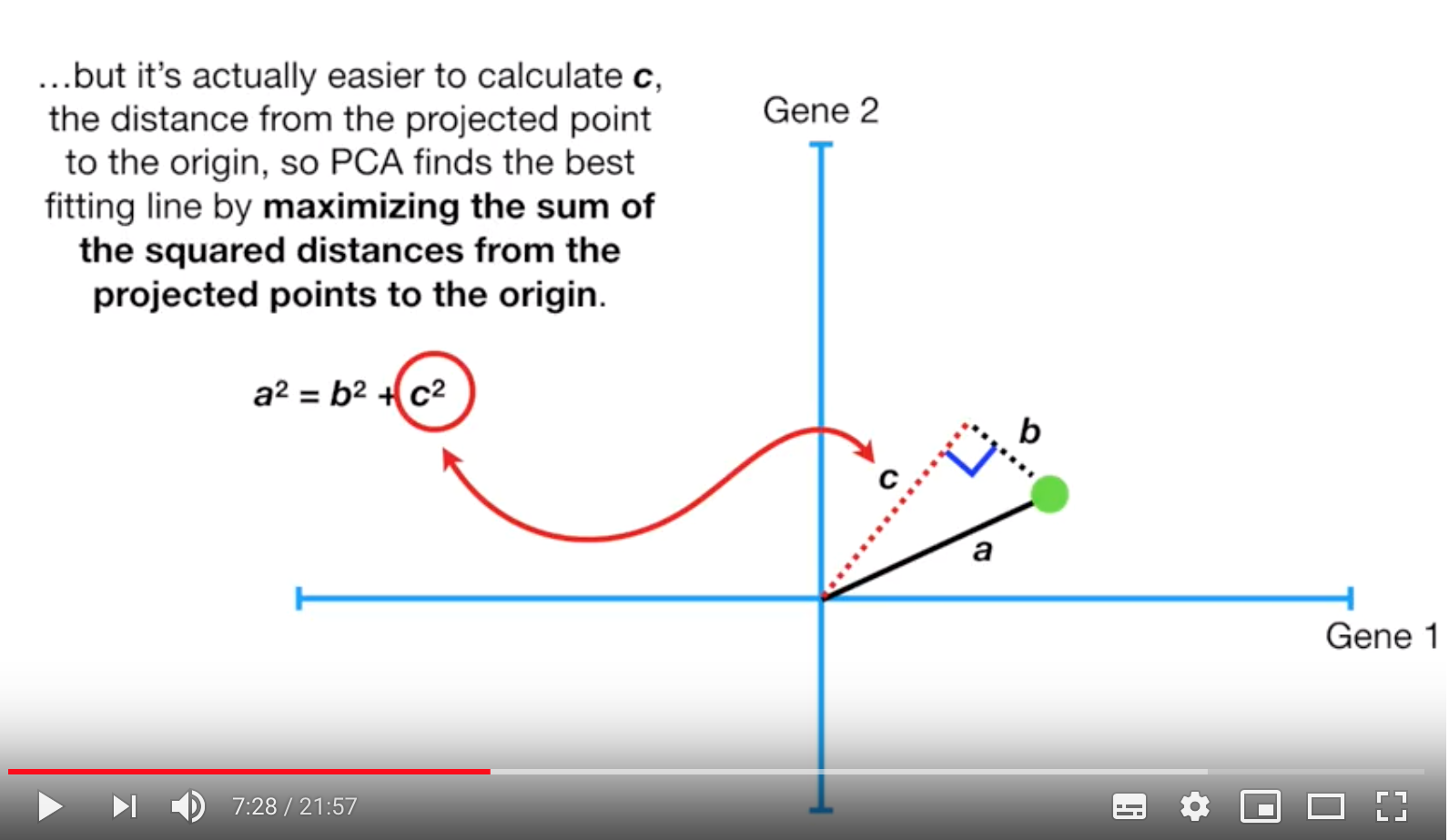
假如現在座標上有個綠色的點，以座標\((0, 0)\)原點，其長度為 a（影片沒有表示這是 a 向量，方便起見，後面以 a, b, c 向量表示），c 向量為 a 向量的投影方向與長度。根據畢氏定理，可以畫出一個正三角形，現在三角形的三邊長分別為 a, b, c（因為我懶得再圖上修正了，現在又變回長度）。而 PCA 要找的投影向量就是，最小化 \(b^2\) 的值，或是最大化 \(c^2\) 的值。

• 投影

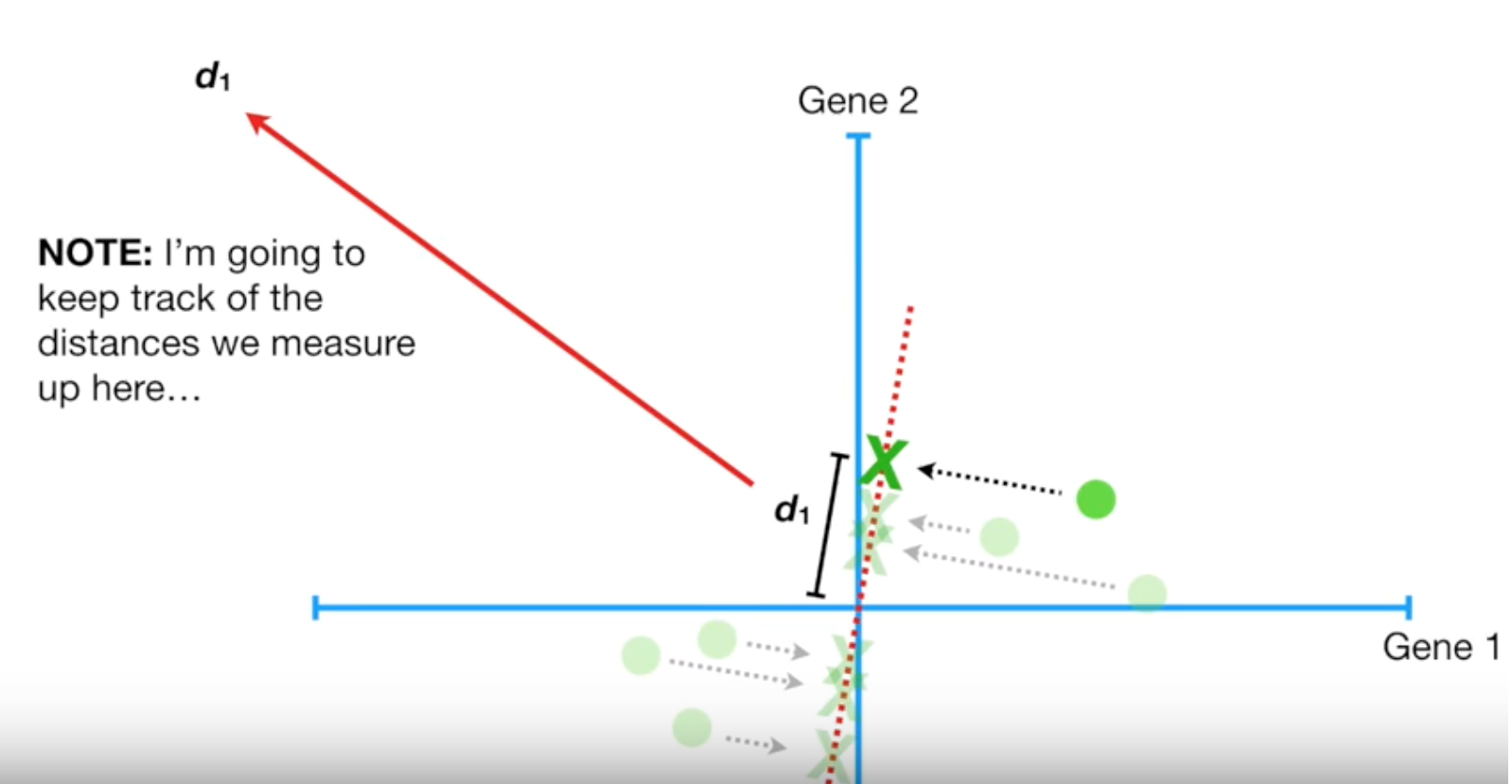
根據上圖，這個二維座標上有好幾個點，我們現在就是要找到一條能讓投影後 variance 最大的投影向量（紅色虛線），如下圖。要找到 SS（eigenvalue） 最小的投影向量。

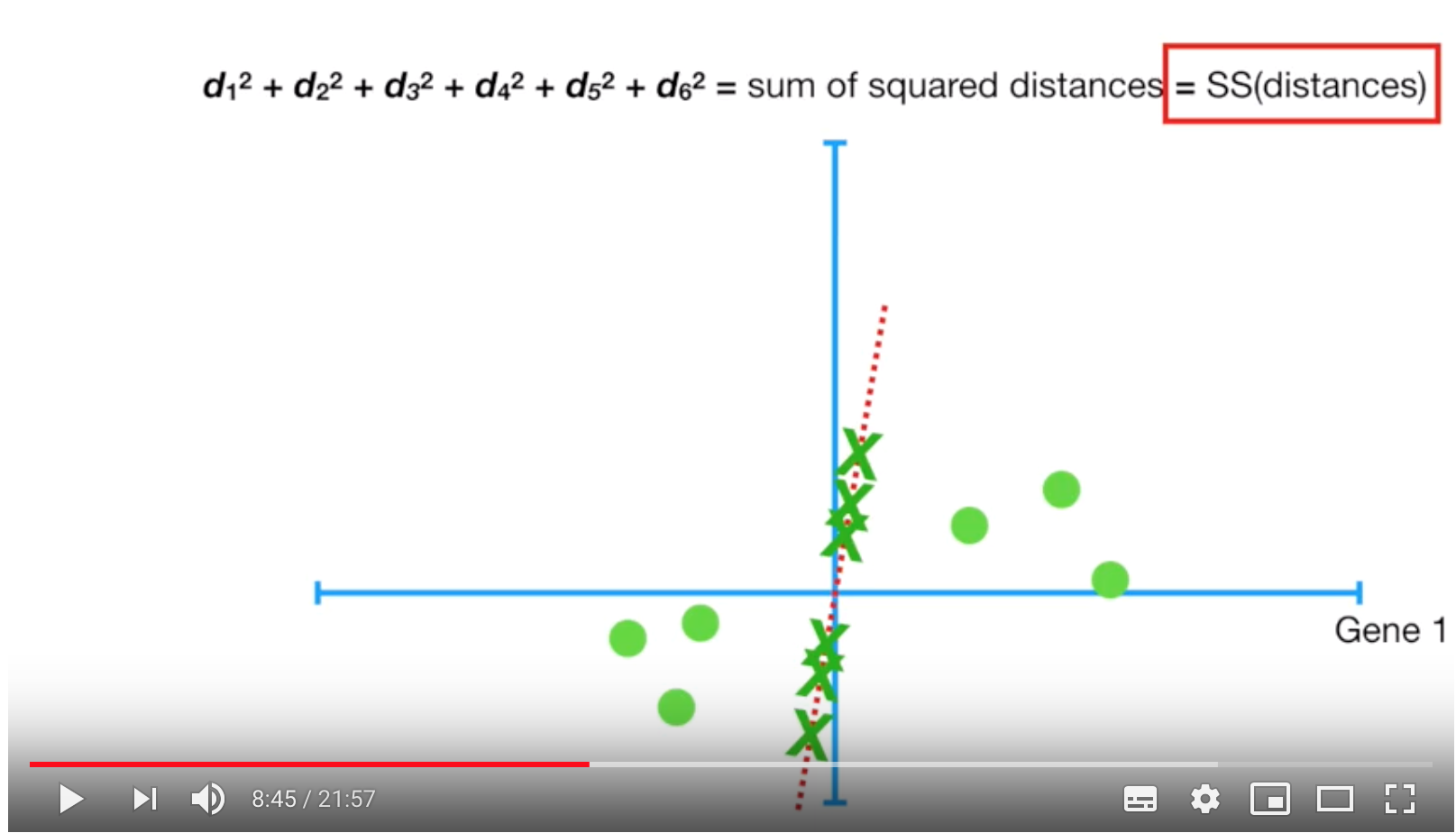
在投影前，我們會先將資料平移 \(x_i - \mu_i\)，也就是不改變點之間的相對位置，這樣不但不會影響找投影向量的結果，在計算上也比較容易。

---

Variation 變異量

變異量 = \(SS/(n-1), n \)是點的數量

有了變異量以後，我們通常會想要知道每個投影向量的變異量占比。

假如現在有 PC1 其變異量為 15，PC2 的變異量為 3，則 PC1 與 PC2 的變異量總和為 18。

所以 PC1 = 15*100%/18 = 83%，PC2 = 3*100%/18 = 17%。

在做 PCA 的時候，我們會根據轉換的 \(PC_i\) 的比重，來決定要考慮要使用幾個 \(PC_i\)。 如果可以解釋百分之九十基本上就可以拿來使用。

假如今天有一筆多維度的資料，但轉換後 PC1 與 PC2 可以表示百分之九十的變異量，那麼這時候只要使用 PC1 與 PC2 就好，且還可以在平面座標上看點的分佈。

---

基本上 PCA 就是在做座標變換，將原變數投影成新變數。接著以最少的新變數來代表原始資料最大的成分（variation 涵蓋量最大）。

其原則如下

• 新變數是原變數的線性組合
• 保留原變數間的最大變異量（variance）

---

Reference:
StatQuest: Principal Component Analysis (PCA), Step-by-Step
機器/統計學習:主成分分析(Principal Component Analysis, PCA)
wikipedia - 主成分分析
The Elements of Statistical Learning
Pattern Recognition and Machine Learning