Linear Regression 屬於 Supervised Learning(監督式學習)，用來預測連續型(continuous)的變數。

---

Simple Linear Regression

Simple Linear Regression 假設 \(X, Y\) 存在線性關係，且可以使用以下的式子來表示 \(X, Y\)的關係。

\[Y \approx \beta_0 + \beta_1 X\]

而現實中我們無法知道參數 \(\beta_0, \beta_1\)，這時候我們會使用 train data 找出估計參數 \(\hat{\beta_0}, \hat{\beta_1}\)。簡單線性回歸的估計式可以寫成，

\[\hat{y} = \hat{\beta_0} + \hat{\beta_1} x\]

其中，\(\hat{y}\) 是當 \(X = x\) 時 \(Y\)的預測值。

---

Estimating the Coefficients

現在有一堆 data， \((x_i, y_i), \thinspace i = 1, 2, 3, …, n\)，根據上面的迴歸式可以將這些 data 表示成，

\[y_i \approx \hat{\beta_0} + \hat{\beta_1} x_i, \thinspace for \thinspace i = 1, 2, 3, ..., n\]

已經知道迴歸模型可以用上面的式子表示，那現在的任務是要找到 \(\hat{\beta_0}\) 和 \(\hat{\beta_1}\)，只要找到這兩個參數就可以預測 \(y\) 了。

找 \(\hat{\beta_0}, \hat{\beta_1}\) 的方法叫 The Least Square Method（最小平方法）。

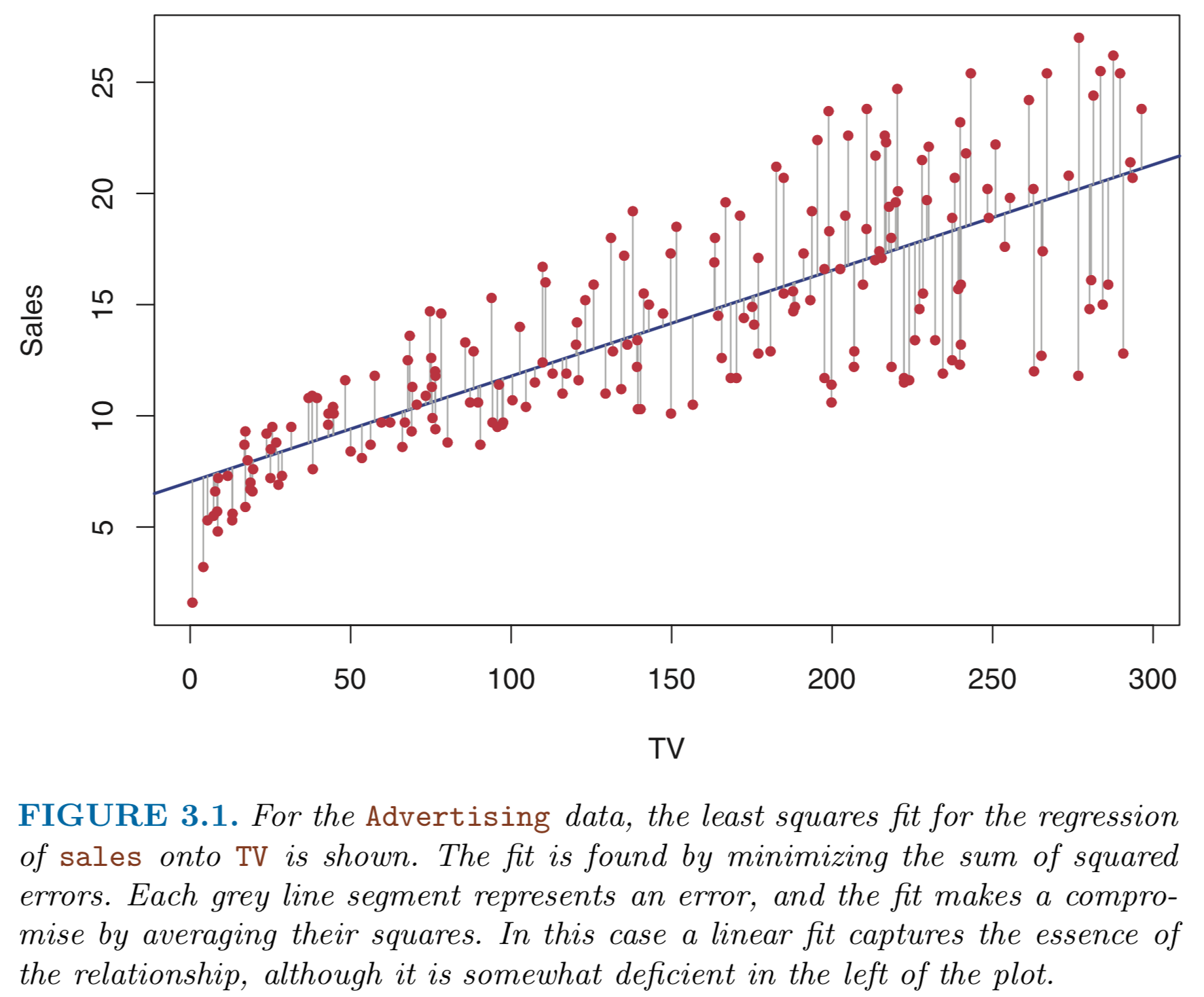
以上圖為例，紅色的點為 observations，深藍色的線是用最小平方法找到的迴歸線。

---

The Least Square Method 是什麼？

式子 \( \hat{y_i} = \hat{\beta_0} + \hat{\beta_1} x_i \) 為 \(X = x_i\) 時 \(Y\) 的預測值。

我們使用 Residual(殘差) 來看這個預測的結果與實際數值的差距，定義為 \(e_i = y_i - \hat{y_i}\) (上圖中紅點到深藍色線的灰色線段們)。

將所有 Residual 相加便能

RSS =

---

Reference:
An Introduction to Statistical Learning with Applications in R