這一系列我是以 Wackerley, Mendenhall and Scheaffer 的
Mathematical Statistics with Applications, 7th edition 這本書為主，
有些名詞與定理解釋會再參考其他書籍與網路作為輔助（下方有參考連結）。

這一篇要介紹常見的離散型分佈（Discrete Distribution），這篇主要是參考 Source

---

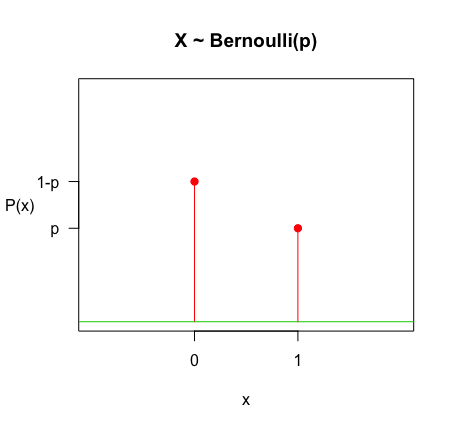
伯努利分佈 Bernoulli Distribution

定義 Definition

• A random variable \(X\) is said to be a bernoulli random variable with peremeter \(p\), shown as \(X \sim Bernoulli(p)\), if its PMF is given by

\[P_X(x) = \left\{ \begin{array}{rcl} p,& \;for\; x = 1 \\ 1-p,& \;for\; x = 0 \\ 0,& otherwise \\ \end{array}\right.\]

• where \(0 < p < 1\)

簡單來說，一個事件只有兩種可能。

生活中有非常多的例子都會是 Bernoulli Distribution，譬如，

1. 考試有及格、不及格
2. 丟擲一枚銅板有正面、反面
3. 小孩子性別可能是男生、女生

---

幾何分布 Geometric Distribution

定義 Definition

• A random variable \(X\) is said to be a geometric random variable with peremeter \(p\), shown as \(X \sim Geometric(p)\), if its PMF is given by

\[P_X(x) = \left\{ \begin{array}{rcl} p(1-p)^{k-1},& \;for\; k = 1, 2, 3,...... \\ 0,& otherwise \\ \end{array}\right.\]

• where \(0 < p < 1\)

Geometric Distribution 的例子：擲一枚銅板，且此銅板擲到 Head 的機率為 \(p\)。今天擲這枚到出現第一個 Head 為止，則其機率分佈為 Geometric Distribution。
另外，每一次擲這枚銅板都會是獨立的 Bernoulli 試驗。

所以，Geometric Distribution 就是很多次的 Bernoulli 試驗直到成功為止。

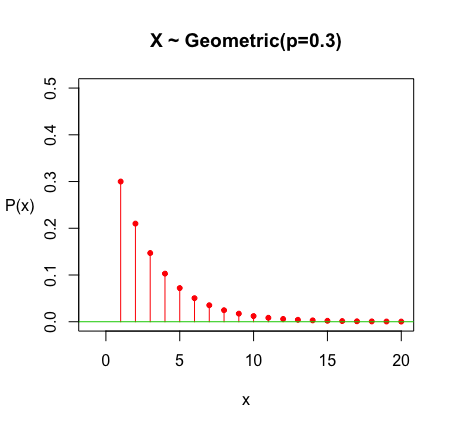
以 \(p = 0.3\) 為例，其 Geometric Distribution 的 PMF 會是這樣，

---

二項分布 Binomial Distribution

定義 Definition

• A random variable \(X\) is said to be a binomial random variable with peremeter \(n\) and \(p\), shown as \(X \sim Binomial(n, p)\), if its PMF is given by

\[P_X(x) = \left\{ \begin{array}{rcl} \left( \begin{array}{c} n \\ k \end{array} \right) p^k(1-p)^{n-k},& \;for\; k = 0, 1, 2,..., n \\ 0,& otherwise \\ \end{array}\right.\]

• where \(0 < p < 1\)

Binomial Distribution 也是很多次獨立 Bernoulli 試驗的結果，但和 Geometric Distribution 不一樣的是，Binomial Distribution 會執行 \(n\) 次的 Bernoulli 試驗，且成功了 \(k\) 次。

所以它的 PMF 會有 \(\left( \begin{array}{c} n \\ k \end{array} \right)\)，表示執行了\(n\) 次，其中有 \(k\) 次成功，且這 \(k\) 次並沒有限定在哪個位置。

可以以丟擲 \(n\) 枚銅板來想，其中 \(k\) 枚硬幣為 Head，\((n-k)\) 為 Tail。

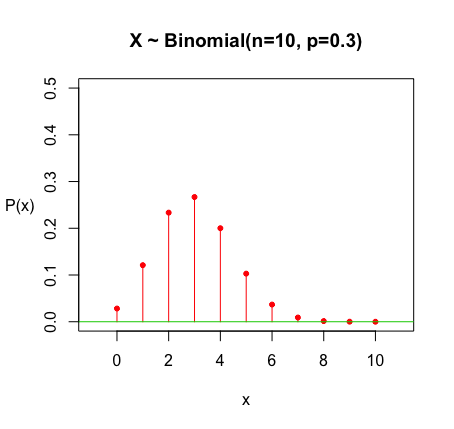
以 \(n = 10,\; p = 0.3\) 為例，其 PMF 圖會是，

Binomial random variable as a sum of Bernoulli random variables

• If \(X_1,\;X_2,\;X_3,…,\;X_n\) are independent \(Bernoulli(p)\) random variable, then the random variable \(X\) defined by \(X = X_1 + X_2 + X_3 + … + X_n\) has a \(Binomial(n,p)\) distribution.

也就是，二項分布可以看成是每個獨立的伯努利分佈的和。

---

布瓦松分布 Poisson Distribution

定義 Definition

• A random variable \(X\) is said to be a poisson random variable with peremeter \(\lambda\), shown as \(X \sim Poisson(\lambda)\), if its range is \(R_X = \{ 0, 1, 2, 3,… \} \), and if its PMF is given by

\[P_X(x) = \left\{ \begin{array}{rcl} \frac{e^{-\lambda} \lambda^k}{k!} ,& k \in R_X \\ 0,& otherwise \\ \end{array}\right.\]

Poisson Distribution 的意義為：單位時間內，事件出現平均 \(lambda\) 次的機率分布。

既然上面的式子為 PMF，那我們來檢驗 \(\sum_{k \in R_X}{P_k(x)} = 1\) 是否正確。

\[\begin{align} \sum_{k \in R_X}{P_k(x)} &= \sum_{k=0}^{\infty} \frac{e^{-\lambda} \lambda^k}{k!} \\ &= e^{-\lambda} \sum_{k=0}^{\infty} \frac{\lambda^k}{k!} \\ \end{align}\]

Note: 根據 Taylor Series(泰勒展開式) \(\; e^{x} = \sum_{k=0}^{\infty} \frac{x^k}{k!}\)，上列式子可以寫成，

\[\begin{align} &= e^{-\lambda} e^{\lambda} \\ &= 1 \\ \end{align}\]

Example:

The number of emails that I get in a weekday can be modeled by a Poisson distribution with an average of 0.2 emails per minute.

1. What is the probability that I get no emails in an interval of length 5 minutes?
2. What is the probability that I get more than 3 emails in an interval of length 10 minutes?

Poisson as an approximation for binomial

• Let \(X \sim Binomial(n, p = \frac{\lambda}{n})\), where \(\lambda > 0\) is fixed. Then for any \(k \in {0, 1, 2,…} \), we have

\[\lim_{n \rightarrow \infty} P_X(k) = \frac{e^{-\lambda} \lambda^k}{k!}\]

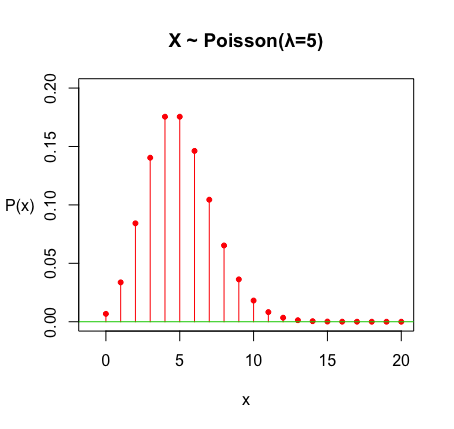
\(X \sim Poisson(\lambda = 5)\) 的函數圖形，

---

參考：

• Mathematical Statistics with Applications 7th Edition
• Introduce To Proability, Statistics and Random Process
• 陳鍾誠的網站