[統計]離散型(Discrete)隨機變數與其機率分佈(1)
這一系列我是以
Wackerley, Mendenhall and Scheaffer 的
Mathematical Statistics with Applications, 7th edition 這本書為主,
有些名詞與定理解釋會再參考其他書籍與網路作為輔助(下方有參考連結)。
這篇內容為書中的 3.1 與 3.2。
在開始前,何謂「隨機變數」?
隨機變數 Random Variable
定義 Definition
- 隨機變數 \(X\) 是一個以樣本空間 \(S\) 為定義域(Domain)的實數值函數。 Source
- A random variable \(X\) is a funcion from sample space to real number. Source
\( X: S \to {\Bbb R}, \ S \ is \ sample \ space \)
\( i.e. \ \forall \ s \in S, \ X(s) \in {\Bbb R} \)
Example:
擲兩枚硬幣,其樣本空間為 \( R = \{HH, HT, TH, TT\} \),共有 \(2^2\) 種可能。
若將 H 定義為 1,T 定義為 0,則其隨機變數 \(X\) 的值為 \( \{0, 1, 2\}\)
而隨機變數又分為 1. 離散型 與 2. 連續型,這一章節我們只會討論離散型。
離散型隨機變數 Discrete Random Variable
定義 Definition
- A random variable \(Y\) is said to be discrete if it can assume only a finite or countably infinite number of distinct values. (DEFINITION 3.1)
- \(X\) is a discrete random variable, if its range is countable. Source
根據定義,離散型隨機變數(Discrete Random Variable)必須為可數(countable)。
所以像是擲銅板或是擲骰子就會是離散型隨機變數。
以擲一顆骰子一次為例,其可能值為 \(\{1, 2, 3, 4, 5, 6\}\), 我們用 \(X\)來表示其隨機變數,
但因為隨機變數為 function,所以我們可以用 \(R_X\)來表示它的範圍,
\( Range(X) = R_X = \{1, 2, 3, 4, 5, 6\} \)
機率質量函數 Probability Mass Function (PMF)
定義 Definition
- Let \(X\) be a discrete random variable with range \(R_X = \{ x_1, x_2, x_3,… \} \) (finite or countably infinite). The function
- is called the probability mass function (PMF) of \(X\). Source
機率質量函數 Probability Mass Function (PMF) 可以用來表達樣本空間中某事件的機率。
譬如說,擲一顆公平的骰子,骰子點數為 1 的機率我們可以這樣表示,
\( P(X = 1) = 1/6 \)
另外,\( P_X(x) \)還有兩個很重要的性質 Source,
- \( 0 \leqslant P_X(x) \leqslant 1 , \forall x \)
- \( \sum_{\substack{x \in R_X}}P_X(x) = 1 \)
簡單來說就是,
- 任何事件發生的機率都只會介於 0 和 1 之間
- 所有事件機率總和等於 1
離散型 PMF 圖
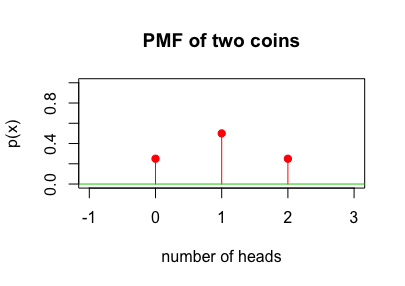
擲兩枚硬幣,出現 head 為 1,tail 為 0 ,其 PMF 函數為
\[P_X(x) = \left\{ \begin{array}{rcl} 1/4,& \;for\; x = 0 \\ 1/2,& \;for\; x = 1 \\ 1/4,& \;for\; x = 2 \\ 0,& otherwise \\ \end{array}\right.\]
函數圖為,
參考:
