在進入連續型隨機變數（Continuous Random Variable）前先插播介紹何謂 CDF。

---

CDF (Cumulative Distribution Function)

定義 Definition

• The cumulative distribution function (CDF) of random variable \(X\) is defined as

\[F_X(x) = P(X \leq x), \forall x \in {\Bbb R}\]

Source

Mathematical Statistics with Applications 這本書將 CDF 稱為 distribution function，
wikipedia 則翻譯為累積分布函數。

以下再分 1.離散型函數 與 2.連續型函數 來看，

---

離散型隨機變數的 CDF

以擲兩枚硬幣為例，出現 head 為 1，tail 為 0，
其隨機變數 \(X\) 的 PMF 函數為

\[P_X(x) = \left\{ \begin{array}{rcl} 1/4,& \;for\; x = 0 \\ 1/2,& \;for\; x = 1 \\ 1/4,& \;for\; x = 2 \\ 0,& otherwise \\ \end{array}\right.\]

PMF 函數圖為，

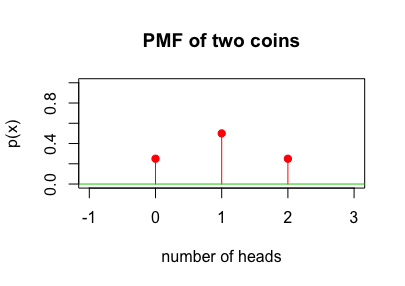
則它的 CDF 累積分佈函數為 \(F_X(x) = \left\{ \begin{array}{rcl} 0,& &for\; x < 0 \\ 1/4,& &for\; 0 \leq x < 1 \\ 3/4,& &for\; 1 \leq x < 2 \\ 1,& &for\; x \geq 2\\ \end{array}\right.\)

CDF 函數圖為，

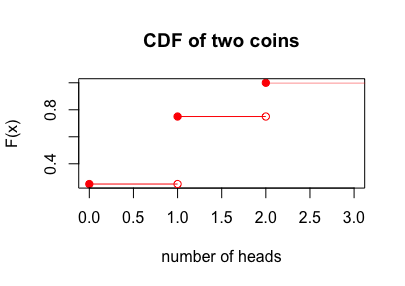
可以發現，離散型的 CDF \(F_X(x)\) 為不連續的函數圖。

關於離散型的 CDF 這影片有更詳細的說明。

---

連續型隨機變數的 CDF

那如果今天有個隨機變數 \(X\)，它的 CDF \(F(X)\) 為連續函數呢？

定義 Definition

• A random variable \(X\) with CDF \(F(X)\) is said to be continuous if \(F(X)\) is a continuous function for all \(X \in {\Bbb R} \). Source

---

參考：

• Introduce To Proability, Statistics and Random Process

---